Chord Intersections
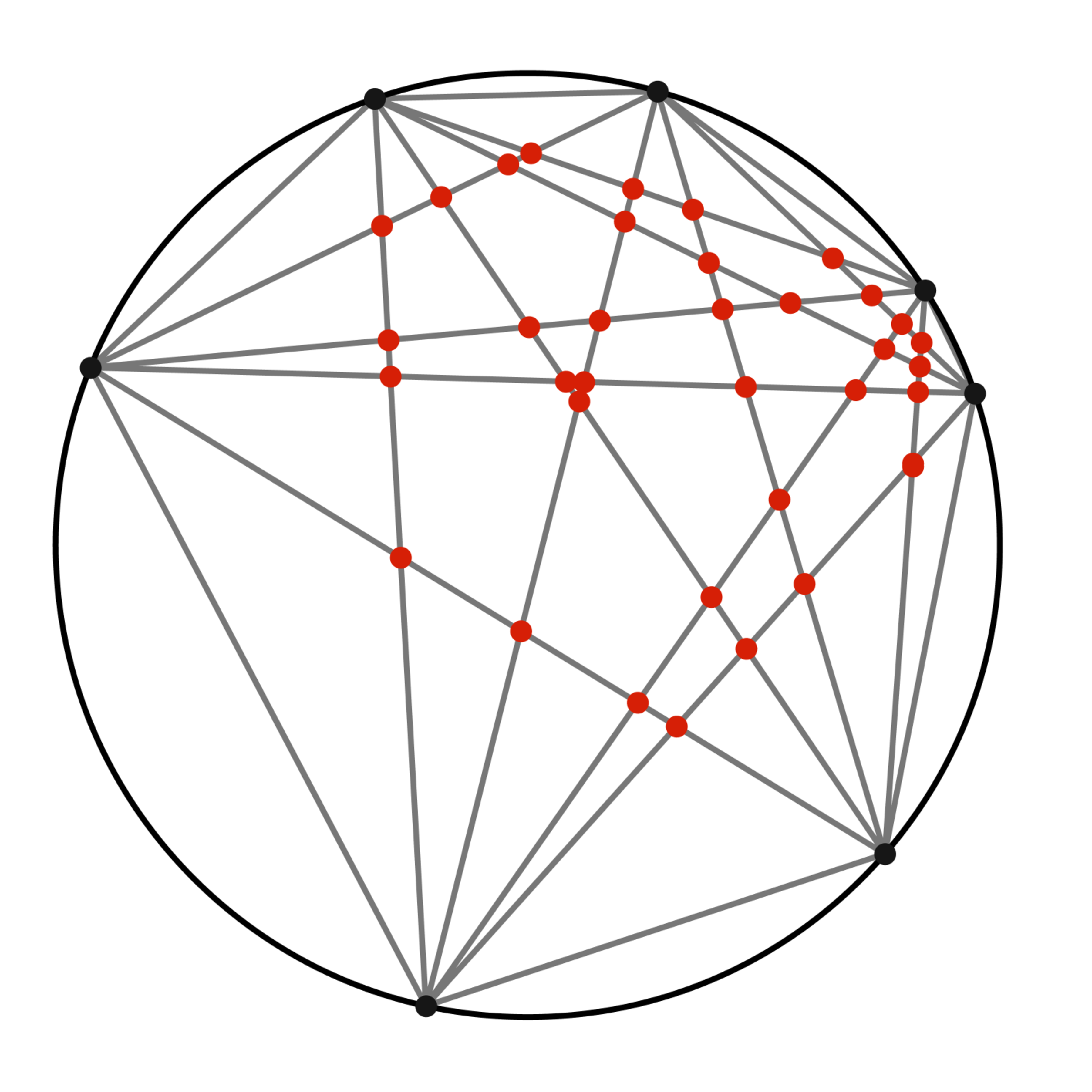
On a circle, points are being connected, each to each other, by chords. Assuming that no three chords meet in a common point, how many points of intersection (within the circle) are formed?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From an intersection point, trace back along the chords to find four endpoints on the circle. Also, any such group of 4 (out of n ) uniquely determines an intersection point. So there is a one-to-one correspondence between points of intersection and (unordered) groups of 4 points. The total number of such groups is the binomial coefficient ( 4 n ) , or 2 4 n ( n − 1 ) ( n − 2 ) ( n − 3 ) .
(In the example, where n = 7 , there are ( 4 7 ) = 4 ! 7 × 6 × 5 × 4 = 3 5 intersections.)