Chord or Tangent???
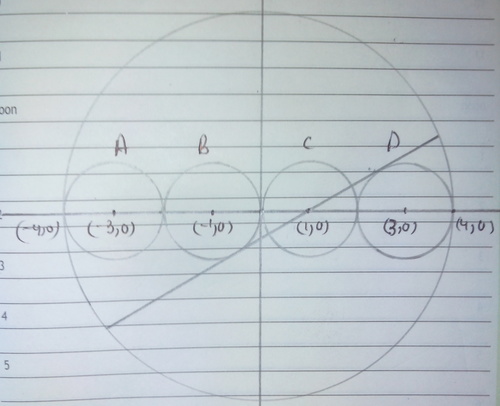 There are 4 circles namely A, B, C & D (as shown in figure) of radius 1 cm each and centres at (-3,0)(-1,0) (1,0) & (3,0) respectively consribed in a bigger circle of radius 4 and centre at (0,0) Chhord of the bigger cirlce is tangent to the circle B and passes through the centre of cirlce C. The Length of the Chord is
x
. Find
x
.
There are 4 circles namely A, B, C & D (as shown in figure) of radius 1 cm each and centres at (-3,0)(-1,0) (1,0) & (3,0) respectively consribed in a bigger circle of radius 4 and centre at (0,0) Chhord of the bigger cirlce is tangent to the circle B and passes through the centre of cirlce C. The Length of the Chord is
x
. Find
x
.
The answer is 63.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
name the centre of cirlce C as O and of circle D as P....
Join PD. Sin ∠ DCP = 1/2
therefore ∠ DCP = 30' = Slope of the chord = m
as we know y=mx+c. putting value of m and satisfying with the point (1,0)
we get c=- 3 1
therefore the equation of chord y= 3 1 (x-1) -----------1
the equation of bigger circle is x 2 + y 2 = 16 ----------2
solving equation 1 and 2 we get x= 4 1 ± 3 2 1 & y= 4 3 − 3 ± 3 2 1
by distance formula on these four points we get the length of chord as 6 3 So the answer is 6 3
i did same :)
Therefore we can say- Slope of chord = t a n ( 3 0 ∘ ) = 1 / 3
Thus by using point-slope form of a line, the equation of chord becomes:
( y − 0 ) y 3 x − 1 − y = ( 1 / 3 ) ( x − 1 ) = 3 x − 1 = 0
Therefore now consider a perpendicular AP is dropped from the centre of the bigger circle i.e ( 0 , 0 ) .
Join point A to any one of the ends of the cord to obtain a right triangle A P Q
Now usin pythagoras theorem and Distance from a point to a line formula :
A P 2 + P Q 2 ⇒ P Q 2 ⇒ P Q 2 ⇒ P Q = A Q 2 = A Q 2 − A P 2 = 1 6 − ⎝ ⎜ ⎜ ⎛ 1 + 3 1 ∣ ∣ ∣ ∣ 3 0 − 1 − 0 ∣ ∣ ∣ ∣ ⎠ ⎟ ⎟ ⎞ 2 = 2 6 3
Now since we know that when any perpendicular is dropped from the center of a circle to a chord, it divides the chord into two halves.
Therefore: Length of chord = 2 ⋅ P Q = 2 ⋅ 2 6 3 = 6 3
Thus comparing our result with the form given in the question,
x = 6 3