Chords chords chords
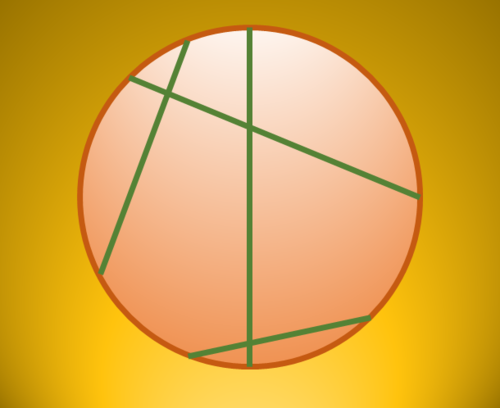 In the circumference of a circle of radius
, two points are chosen with a uniform distribution. The probability that the length of the chord between these two points is less than
is
for coprime positive integers
.
In the circumference of a circle of radius
, two points are chosen with a uniform distribution. The probability that the length of the chord between these two points is less than
is
for coprime positive integers
.
Find .
This problem was from CB Paul Science quiz (Stage round) where it is expected to be solved in 40 seconds.
Try my Other Problems
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
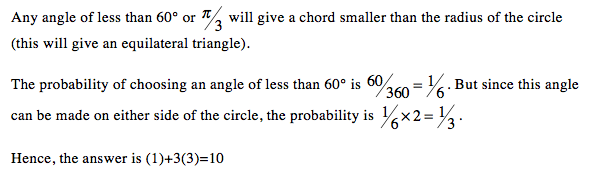
Here's a solution without words:
For those who didn't understand, here's another clue: P = 9 0 ° θ = 3 1 = b a