Chords in a circle

Let $AC$ and $BD$ intersect at $E$ , and let the center of the circle be $O$ so that $OB = OC = 6$ .

Since central $\angle BOC$ subtends the same arc as inscribed $\angle BDC$ , $\angle BOC = 2 \cdot \angle BDC = 2 \cdot 45° = 90°$ .

From right isosceles $\triangle BOC$ , $BC = 6\sqrt{2}$ , and from right isosceles $\triangle EDC$ , $EC = \frac{10}{\sqrt{2}}$ .

Then by the Pythagorean Theorem on $\triangle BEC$ , $BE = \sqrt{(6\sqrt{2})^2 - (\frac{10}{\sqrt{2}})^2} = \sqrt{22}$ , so that from right isosceles $\triangle ABE$ , $AB = \sqrt{22} \cdot \sqrt{2} = \sqrt{44}$ .

Therefore, $N = \boxed{44}$ .

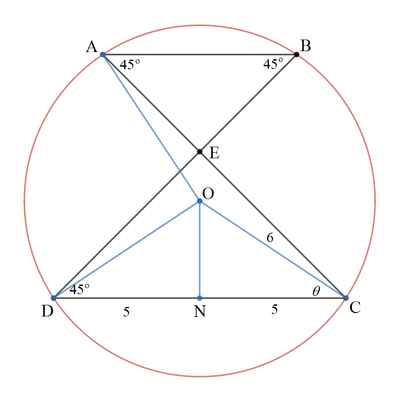
Let $AC$ and $BD$ intersect at $E$ , the center of the circle be $O$ , and $ON$ be perpendicular to $CD$ . Then $CN = DN = 5$ , and $ON = \sqrt{OC^2-CN^2} = \sqrt{6^2-5^2} = \sqrt{11}$

Let $\angle OCD = \angle ODC = \theta$ . Then

$\begin{aligned} AC & = 2 \cdot OC \cdot \cos \angle OCE = 2 \cdot 6 \cos (45^\circ - \theta) \\ & = 12 (\cos 45^\circ \cos \theta - \sin 45^\circ \sin \theta) \\ & = 6\sqrt 2 \left(\dfrac 56 - \dfrac {\sqrt{11}}6 \right) = 5\sqrt 2 - \sqrt{22} \\ AE & = AC - CE = 5\sqrt 2 - \sqrt{22} - CD \cos 45^\circ = 5\sqrt 2 - \sqrt{22} - 5\sqrt 2 = \sqrt{22} \\ \implies AB & = AE \cdot \sec 45^\circ = \sqrt{22} \cdot \sqrt 2 = \sqrt{44} \end{aligned}$

Therefore $N = \boxed{44}$ .

Let O be the centre of the circle, let M be the midpoint of AB and N be the midpoint of CD, and let P be the intersection of AC and BD. Furthermore, let AM = half of AB be $x$ .

ND = 10/2 = 5, and OD = 6 (radius), so ON = $\sqrt{6^2-5^2} = \sqrt{11}$ . Meanwhile, DN = PN, so PN = 5, and similarly, MP = x. Thus OP = PN - ON = $5 - \sqrt{11}$ .

Now $AM, PO$ form the legs of a right triangle, and $AO$ is the hypotenuse. $AO = 6$ as it is also a radius. Hence $x^2 + (x + 5 - \sqrt{11})^2 = 6^2$ , so $x^2 + x^2 + 2(5 -\sqrt{11})x + 36 - 10\sqrt{11} = 36 \Rightarrow 2x^2 + (10 - 2\sqrt{11})x - 10\sqrt{11} = 0 \Rightarrow x^2 + (5 - \sqrt{11})x - 5 \sqrt{11} = 0$ .

Factorising gives $(x + 5)(x - \sqrt{11}) = 0 \Rightarrow x = -5, \sqrt{11}$ . Since $x$ has to be positive, $x = \sqrt{11}$ only. Finally, remember that $AB = 2x = 2 \sqrt{11} = \sqrt{44}$ , hence $N = \boxed{44}$ .

Let circle center is O, CD's midpoint is M and AC's midpoint is N, intersection of AC and BD is P: $\\ OM = \sqrt {{OC}^2 - (\frac {CD}2)^2} = \sqrt {6^2 - 5^2} = \sqrt {11} \\ PM = \frac {CD}2 = 5 \\ OP = PM - OM = 5 - \sqrt {11} \\ ON = \frac {OP}{\sqrt 2} = \frac {5 - \sqrt {11}}{\sqrt 2} \\ AN = \sqrt {{AO}^2 - {ON}^2} \\ = \sqrt {6^2 - (\frac {5 - \sqrt {11}}{\sqrt 2})^2} = \frac {5 + \sqrt {11}}{\sqrt 2} \\ AP = AN - PN \\ = \frac {5 + \sqrt {11}}{\sqrt 2} - \frac {5 - \sqrt {11}}{\sqrt 2} \\ = \sqrt {22} \\ AB = AP \sqrt 2 = \sqrt {44} \\ \therefore N = 44$