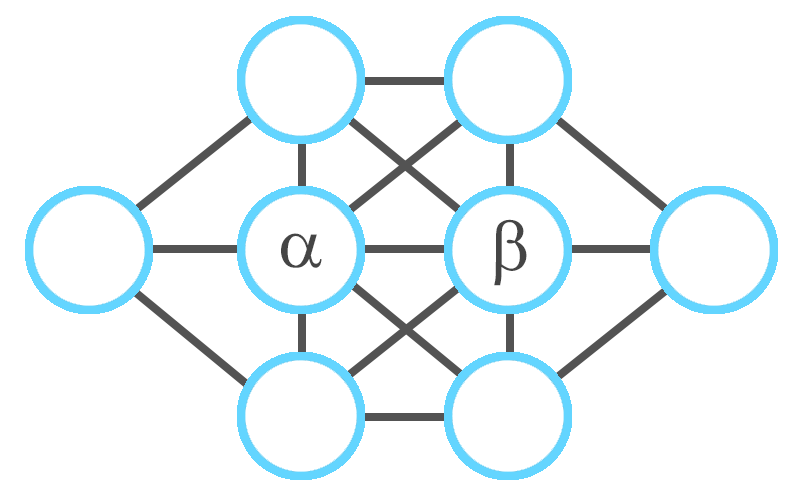
Christmas Streak 04/88: Fill In The Diagram
I want to fill in the eight circles below using each of the numbers 1, 2, 3, 4, 5, 6, 7, 8 exactly once . Additionally, consecutive numbers--e.g. ( 1 , 2 ) or ( 5 , 6 ) -- cannot be placed in circles which are connected by a line segment.
Is this possible, and if so, what is the sum of the two numbers in the middle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Excellent solution and diagram.
Does placing the 1 and 8 uniquely determine the rest of the nodes?
Log in to reply
Not necessarily, the whole picture can be flipped, meaning ( 3 , 5 ) and ( 4 , 6 ) can be interchanged pair-to-pair.
The number α is connected to six other numbers. But for the numbers 2 , … , 7 there are only five non-adjacent values. Therefore α must be either 1 or 8. The same is true for β .
Therefore, if there exists a solution, α + β = 1 + 8 = 9 .
Once we have 1 and 8 in the middle, it is not difficult to find a solution.
But how many solutions are there, upto rotations and reflections?
Log in to reply
Name the boxes CL (central left), FL (far left), TL (top left), BL (bottom left), etc.
We know that 1 and 8 are in the center. After optional horizontal reflection, we have C L = 1 , C R = 8 . There is only one possible placement for 2 and 7. F R = 2 , F L = 7 . This leaves two possible positions for 3: either above or below 1. After optional vertical reflection, we get T L = 3 . The situation for 6 is similar: either above or below 8. However, if we place it on top (next to 3), the remaining numbers 4 and 5 would become neighbors. Therefore we are forced to choose B R = 6 , and naturally B L = 4 , T R = 5 .
Because we had the freedom of two independent reflections, there are four solutions, which are essentially the same under reflection.
But can there be other elements placed in those two nodes?
Log in to reply
I just showed that ''It is possible''.
And of course the answer is unique.
elegant and succinct.
What if the arrangement is: 7 5 4 1 3 2 6 8 Then the sum comes out to be 4 which is not a option? Please correct me if I'm mistaken.
Log in to reply
Look carefully:
7 5 4 1 3 2 6 8
2 and 3 are consecutive digits.
4 and 5 are consecutive digits.
First, after trying a few randomly, I realized that I could use the potential answers to help guide me. In order to be possible, I would need the middle two numbers to add up to one of the sums given: 3,7,9, or 10. This means that I have a limited number of possible values for the two central circles as follows:
- 3=1+2>>This is impossible since it would place 1 and 2 next to each other.
- 7=1+6=2+5=3+4
- 9=1+8=2+7=3+6=4+5
- 10=1+9=2+8=3+7=4+6=5+5
Right away, I noticed that I could eliminate (3,4), (4,5), and (5,5) since they are next to each other or use a number twice which violate the given rules. This leaves me with:
- 7=1+6=2+5
- 9=1+8=2+7=3+6
- 10=1+9=2+8=3+7=4+6
Next, I tested out (1,6) and then (2,5) and realized that I would always have two possible numbers that wouldn't work because 6 is between 5 and 7 or because 5 is between 4 and 6. This led me to realize I could eliminate everything except the following because 8 only can't have a 7 next to it:
- 9=1+8
- 10=2+8
Then I tested both and realized that only the first option works and would need to be arranged as follows:
Best solution so far.
The numbers with the fewest connections 1, and 8 must go in the circles with the most connections, the two marked center circles, to avoid consecutive numbers in adjoining circles.
Both middle nodes are connected to six other nodes, thus we can rule out any of the interior numbers ( 2, 3, 4, 5, 6, 7). We can do this because we know that any interior number must be adjacent to two other numbers. Consequently, only 1 and 8 can fill the middle node slot. From here we can fill in the rest of the graph to prove it can be solved.
α and β only have 1 path each (path being a circle not connected) which means they must be at the start and end, which is 1 and 8 so the answer is 9
Ther are four possible ways
• 5.3.... .....2.8.1.7.... ....6.4.
• 3.5... .......7.8.1.2...... ....4.6.
• 6.4.... ......2.8.1.7...... ....5.3.
• 4.6... .......7.8.1.2........ . 5.3.
My challenge to you is to find any other possibility i am sure you can't Pls post if you can Join with me on ;- [email protected]
Thus the answer is 1+8. (=9) Also this kind of sets are possible to get
Anyone takingnthis challenge
I tried the brute force and quickly found out the alpha and beta has to be numbers who can connect to 6 non adjacent numbers uniquely. Only 1 and 8 fit as these are the only numbers with 1 adjacent number which can be placed on the opposite sides.
I think it may be useful to explain the reasoning behind how the diagram can be filled in, after realizing that either alpha or beta must be 1, and the other must be 8.
First, note that the empty diagram is symmetric. Thus, it is possible to set alpha to 1 and beta to 8 without loss of generality. After this is done, note that 2 must be in the cell not touching 1, and 7 must be in the cell not touching 8. Thus we have filled in the central column.
There are four remaining cells, to be filled in with 3, 4, 5, and 6. Note that 4 and 5 may be placed in any of these cells, but 3 and 6 are limited to only two cells, because their respective consecutive numbers are filled in. To make the next step more efficient, then, choose either 4 or 5 to fill in, as either one will immediately force the placement of either 3 or 6, by leaving only one place for one of them to go.
I arbitrarily chose to fill in the cell above 1 with 4. Thus the cell below 1 must be 3. Thus the cell below 8 must be 5. Thus the cell above 8 must be 6. Thus it is possible to fill in the diagram in at least one way. I hope this helps!
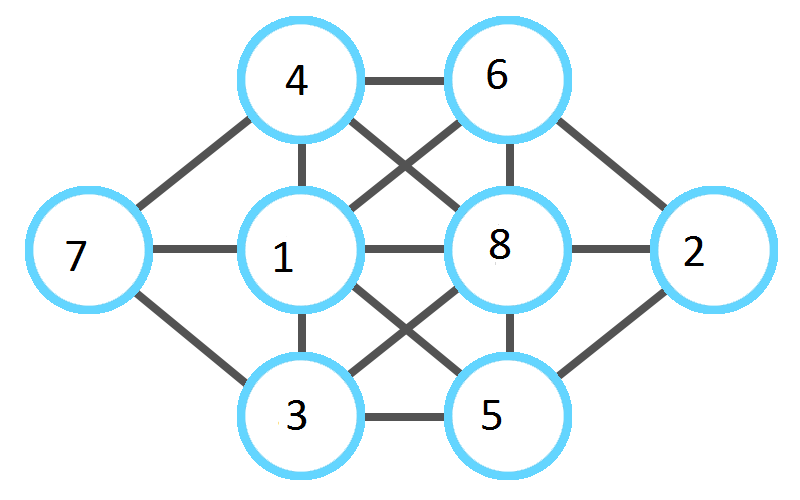
The reasoning is simple.
If we choose a number other than 1 or 8 and put it into the center of the diagram( α , β ), then, there are two numbers that are adjacent to it.
However, there is only one circle that is not connected to the number, and therefore, it is not possible to fill the diagram.
Then there're only 1 and 8 that can go into the two center circles, so we already know the answer is 9 , given that such arrangement(s) of numbers exist(s).
Seems like it's possible, as shown on the right.