Christmas Streak 08/88: Six Lines + Two Circles
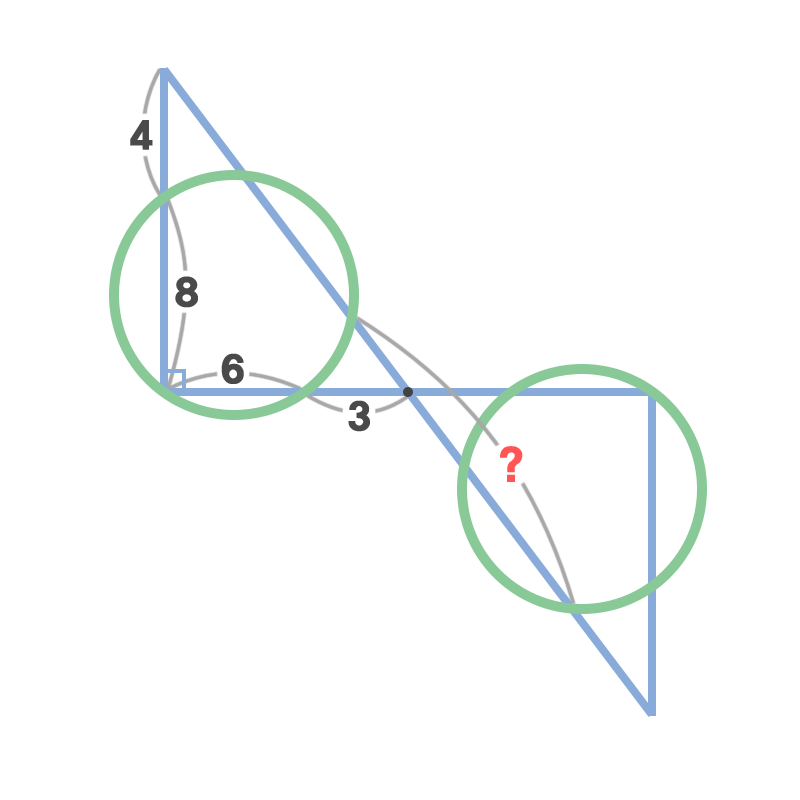
Tom has drawn two right triangles and two circles so that they are perfectly symmetrical around the black point at the center of the diagram.
What is the value for the red question mark ? in the diagram, to three decimal places?
Note:
The image is not drawn to scale.
This problem is a part of <Christmas Streak 2017> series .
The answer is 13.600.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice simple solution. Up voted. I gave my solution just to show a nothere approach.
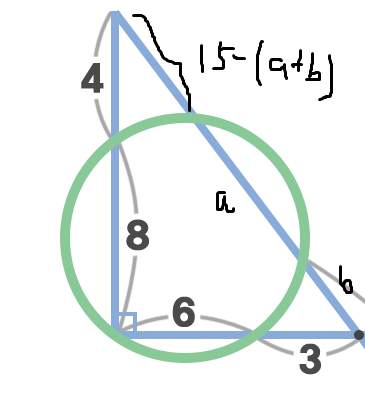
My approach was, since the two triangles are congruent and symmetrical, I just focus on the one circle.
By power theorem,
4(12) = (15 - (a+b))(15 - b) (1)
and
3(9) = (b)(a + b) (2).
The ? is also the same as the value of a + 2b.
Expanding 1 yields: 48 = 225 - 15(a + 2b) + b(a + b). From 2, we can simplify it further to:
48 = 225 + 27 - 15(a + 2b).
∴ a + 2 b = ? = 1 5 2 2 5 + 2 7 − 4 8 = 1 3 . 6 .
Nice and simple approach. Up voted . My solution is just to show different approach.
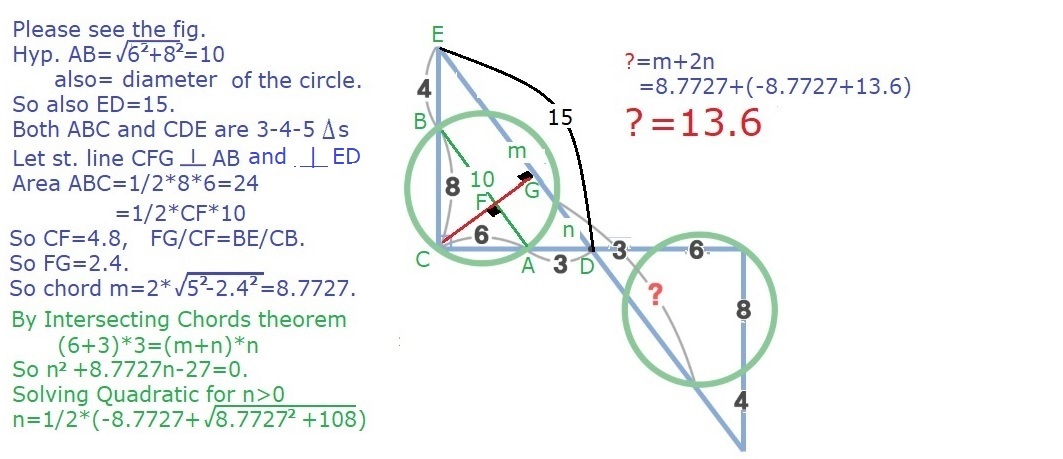
As you can see on the right, using the power theorem , we see that
x ( 1 5 − y ) = 3 ⋅ 9 y ( 1 5 − x ) = 4 ⋅ 1 2
Then, it is not so hard to see that
y ( 1 5 − x ) − x ( 1 5 − y ) 1 5 y − x y − 1 5 x + x y 1 5 ( y − x ) y − x = 4 8 − 2 7 = 2 1 = 2 1 = 1 . 4
Finally, the value of ? is
x + ( 1 5 − y ) = 1 5 − ( y − x ) = 1 5 − 1 . 4 = 1 3 . 6 .