Christmas Streak 23/88: Try Angle Chase
Triangle A B C has side lengths A B = 7 , B C = 8 , C A = 5 .
Trisect each side and create the green triangle in the diagram by connecting the points closest to vertices A , B , C counterclockwise.
The area of the green triangle is a + d b c for integers a , b , c , d , where b and d are positive coprime integers and c is square-free.
Find the value of a + b + c + d .
This problem is a part of <Christmas Streak 2017> series .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
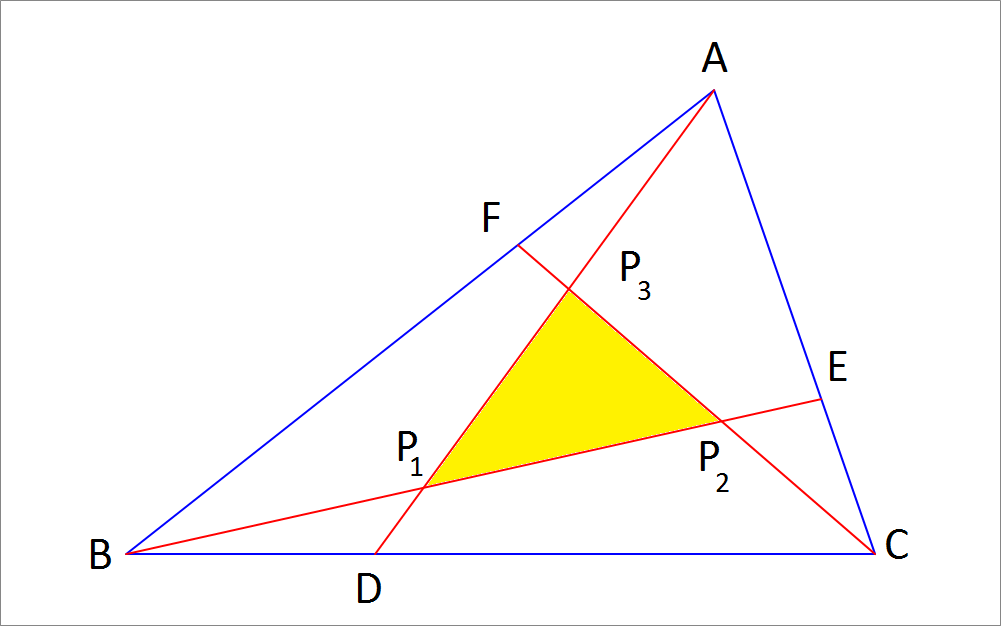
Let the three trisecting points be D, E, and F. Further let the vector u = A B and v = B C , and let's take point A as the origin of the reference frame.
Then, it follows that points on the line A D are given by:
p = x ( u + 3 1 v )
and points on the line BE are given by
q = u + y ( v + 3 1 ( − u − v ) ) = u + y ( − 3 1 u + 3 2 v )
and points on the line CF are given by
r = u + v + z ( − u − v + 3 1 u ) = u + v + z ( − 3 2 u − v )
Intersecting the first two, we obtain the following system of equations,
x = 1 − 3 1 y , a n d 3 1 x = 3 2 y
The second equation implies y = 2 1 x . Substituting into the first equation,
x = 1 − 6 1 x ⇒ x = 7 6
Hence, the point P 1 is given by,
P 1 = 7 6 ( u + 3 1 v ) = 7 6 u + 7 2 v
From symmetry we can deduce the expressions for P 2 and P 3 ,
P 2 = u + 7 6 v + 7 2 ( − u − v ) = 7 5 u + 7 4 v
and
P 3 = u + v + 7 6 ( − u − v ) + 7 2 u = 7 3 u + 7 1 v
To compute the area, we compute the following vectors,
P 1 − P 3 = 7 3 u + 7 1 u
and
P 2 − P 3 = 7 2 u + 7 3 v
And the area of the small triangle is given by
Area = 2 1 ∣ ( P 1 − P 3 ) × ( P 2 − P 3 ) ∣
Note that u × u = 0 and v × v = 0 , hence
Area = 2 1 ∣ 4 9 9 ( u × v ) + 4 9 2 ( v × u ) ∣
Area = 2 1 ∣ ( 4 9 9 − 4 9 2 ) ( u × v ) ∣
Simplifying, and noting that 2 1 ∣ u × v ∣ = Area of triangle ABC
[ P 1 P 2 P 3 ] = 7 1 [ A B C ]
From Heron's formula, we can easily compute the area of ABC, the semi-perimeter is given by,
s = 2 a + b + c = 1 0 , therefore,
[ A B C ] = s ( s − a ) ( s − b ) ( s − c ) = 1 0 ⋅ 2 ⋅ 3 ⋅ 5 = 1 0 3
And finally,
[ P 1 P 2 P 3 ] = 7 1 0 3
making the answer 0 + 1 0 + 3 + 7 = 2 0 .
Assume that the triangle is like this:
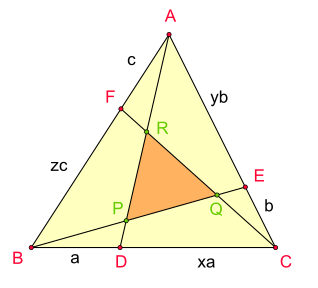
This problem is application of Routh's Theorem.
So, the area of green triangle in the problem ( or orange in the figure ) = A r e a Δ A B C ( ( x y + y + 1 ) ( y z + z + 1 ) ( z x + x + 1 ) ( x y z − 1 ) 2 )
In this problem, we will find out that x = y = z = 2 . So,
Area of green triangle = 2 7 + 5 + 8 ( 1 0 − 7 ) ( 1 0 − 5 ) ( 1 0 − 8 ) ( ( ( 2 ∗ 2 ) + 2 + 1 ) ( ( 2 ∗ 2 ) + 2 + 1 ) ( ( 2 ∗ 2 ) + 2 + 1 ) ( ( 2 ) ( 2 ) ( 2 ) − 1 ) 2 ) = 1 0 ( 3 ) ( 5 ) ( 2 ) ( 7 3 7 2 ) = 7 1 0 3 ⟹ a + b + c + d = 0 + 1 0 + 3 + 7 = 2 0 .
- Suggestion only: I guess, you may use weights here? Is it applicable?
I think weights is good if x, y, z are not equal. It is over kill to use Routh's Theorem in present problem.
F r o m t h e l e f t b o t t o m f i g . w e h a v e , A r e a Δ A B C = 1 / 4 ∗ ( 5 + 7 + 8 ) ∗ ( 5 + 7 − 8 ) ∗ ( 5 − 7 + 8 ) ∗ ( − 5 + 7 + 8 ) = 1 / 4 ∗ 2 0 ∗ 4 ∗ 6 ∗ 1 0 = 1 0 3 . A r e a Δ P Q R = A r e a Δ D C R ∗ R Q / R C ∗ R P / R D = A r e a Δ D C R ∗ 3 Z / 6 Z ∗ 3 Z / 4 Z = 3 / 8 . A r e a Δ D C R = A r e a Δ D C A ∗ R D / A D = A r e a 2 / 3 ∗ Δ A B C ∗ 4 Z / 7 Z ∴ A r e a Δ P Q R = A r e a 3 / 8 ∗ 2 / 3 ∗ 1 0 3 ∗ 4 / 7 = 1 0 3 / 7 = 0 + 1 0 3 / 7 = a + b c / d . a + b + c + d = 0 + 1 0 + 3 + 7 = 2 0
Correction:- In the fig to the right, point G and so line EG is not required.
On second line in the note under this fig , please replace
′ b y Δ .
That is the start of line two:- " S o Δ E B C S D ∣ ∣ . . . . . "
THE APPROACH:-
All three trisectors are near to a side in a similar way. AD near AB, BE near BC, CF near CA. So each trisector is divided
by other two in the same ratio, with constant of proportionality z for AD, x for BC and y for CF.
We found first BP:PE::3:4. Then DP:DR::1:4
Thus for any one trisector say BE we have, distances between,
( vertex to nearest intersection point ):(two intersecting points):(second intersecting point and intersection with opposite side):BP:PQ:QE::3:3:1.
Similarly for CF and AD.
There after calculated the area of triangle ABC and linked it to triangle PQR. This was done knowing Ratio of areas of any two triangles with one common vertex and then one common height between two triangles, using ratios found before. We did by using trisector BE and AD.
When all sides are not divided in equal ratios we will have to use different method for getting ratio we obtained as 1:4. We have to stick to trisector BE for this.
Drawing line EG||AB as shown in the fig. to the right plus another line QN||AB, N on BC. Point K as intersection of EG and QC. First using Triangle QCN and KN||QN. Then using triangle BEG and QN||EG. Using same method for other two cevians. In fact at first I had used this method but switched to above since it is shorter.
This explanation to make it easy for those not familiar with such problems.