Christmas Streak 29/88: Ping Pong!

Logic Level 2

Alyssa, Bill, and Clayton are playing ping pong. The rules are as follows:

  1. The first game is between Alyssa and Bill.

  2. Whenever a game ends, the next game is played with the winner against the person who was sitting out.

  3. No ties are possible.

For example, one possible sequence of results is as follows:

Alyssa defeats Bill.

Clayton defeats Alyssa.

Clayton defeats Bill.

Alyssa defeats Clayton.

After some number of games have been played, they count how many times each player won; Alyssa won 10 times and Bill won 21 times.

How many times did Alyssa and Bill play against each other?

14 15 16 17 Cannot be determined

Boi (보이) by Boi (보이) , 19, South Korea

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

8 solutions

Peter Macgregor
Nov 6, 2017

let X be the number of times A and B play together.

Together A and B win 31 games. These wins include the X games when they play each other, and the games when C is defeated. So we have

X = 31 − (number of times C is defeated) X=31-\text{(number of times C is defeated)}

Now, every time C is defeated A and B have another game, and we know that A and B start with the first game, so we can write

X = (number of times C is defeated)+1 X=\text{(number of times C is defeated)+1} (see note below)

Combining these two equations gives

X = 31 − ( X − 1 ) X=31-(X-1)

which is easily solved to give X = 16 \boxed{X=16}

Note. Careful readers will notice that I have assumed that the last game is between A and B. Assuming instead that C has the last game removes the +1 term in this equation. But then we find that A and B play X = 31 2 = 15 1 2 X= \frac{31}{2}=15\frac{1}{2} games which can be ruled out as ridiculous!

41 Helpful 0 Interesting 0 Brilliant 0 Confused 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
 
import random

def game(p1, p2, tot_A, tot_B, c, counter):
    if c < 30:
        counter += 1
        print
        playing = [p1,p2]
        print 'Game %d\t\t' %counter ,
        print ' '.join(playing),
        if (playing  == ['A', 'B']) or (playing  == ['B', 'A']):
            c += 1
            print '     Match #%d between pair' % c,
        sitting = list(set(players)-set(playing))
        winner = random.choice([p1,p2])
        if winner == 'A':
            tot_A += 1
            print '     A has won %d games     B has won %d games' %(tot_A, tot_B),
        if winner == 'B':
            tot_B += 1
            print '     A has won %d games     B has won %d games' %(tot_A, tot_B),
        y = tot_A + tot_B
        if y == win_thresh:        
            print '\nTotal matches played between A (%d wins total) and B (%d wins total) is %d' % (tot_A, tot_B, c)
        game(winner, sitting[0], tot_A, tot_B, c, counter)



win_thresh = 31

tot_A = 0
tot_B = 0
count = 0
counter = 0

players = ['A','B','C']    
game('A','B', tot_A, tot_B, count, counter)

Michael Fitzgerald - 3 years, 7 months ago

This script is not specific to A winning 10 and B winning 21, but works on number of games won by both totaling 31

Michael Fitzgerald - 3 years, 7 months ago
Boi (보이)
Oct 27, 2017

Answer: 16

Let's fill out the diagram below:

Won Lost Waited
A 10 x
B 21 y
C z

If a person loses, they need to wait during the next game, and therefore the number of loss should be equal to the number of waiting.

However, there're these exceptions:

1. C waits at the first game no matter their win or loss.

2. Whoever loses at the last game doesn't wait.

Therefore, we need to split the cases where A, B, and C loses at the last game, respectively.

If A loses in the last game:

Won Lost Waited
A 10 x x-1
B 21 y y
C z z+1

In the perspective of A, there were 10 + x + (x-1) = 2x + 9 games. And in the perspective of B, there were 21 + y + y = 2y + 21 games.

In the perspective of us, there were x + y + z loss, which means there were x + y + z games.

2x + 9 = 2y + 21 = x + y + z.

Solving this yields z = 15, and therefore C has waited z + 1 = 16 times. This means A and B have played against each other 16 times as well.

If B loses in the last game:

Won Lost Waited
A 10 x x
B 21 y y-1
C z z+1

Similarly, solving the equation that comes out from this also yields z = 15. A and B have played against each other 16 times.

If C loses in the last game:

Won Lost Waited
A 10 x x
B 21 y y
C z z

Solving this, however, yields z = 15.5. This is impossible, so C couldn't have lost the last game.

From above, we can figure out that A and B have played against each other exactly 16 times , and an additional fact that C didn't lose the last game.

14 Helpful 0 Interesting 0 Brilliant 0 Confused

argh...I missed condition 1. I think the answer is "15 or 16" if you remove condition 1.

My solution was as follows: A plays B first. Someone wins a game. Then C plays for awhile, until either A or B wins against him. Then it's A vs. B again. Notice that in the sequence of games starting with A vs. B and ending with C losing, the number of A+B wins combined increases by 2. Call this sequence a "loop."

They combined for 31 wins, so there are 15 loops giving 30 combined wins, and then the 31st win comes from the winner of the 16th A vs. B match at the beginning of the 16th loop.

That's it! I think it's pretty elegant.

Patrick Corn - 3 years, 7 months ago

Log in to reply

Pretty neat indeed!

My solution is the general answer, as to why it must be 16 times, but yeah, your way definitely works too! >w>

Boi (보이) - 3 years, 7 months ago

Beautiful :)

Harsh Agarwal - 3 years, 7 months ago

Let's think Clayton never won. Alyssa wins=10, Bill wins=21. Then total games according to above assumption is 31. And let Alyssa won all first 10 games as given. In first 10 games Alyssa plays against Bill 5 times. In 11th game Alyssa and Bill plays against each other again but let from this time Bill wins all the next 21 games. For 20 games, i.e 11th to 30th game, Alyssa plays against Bill 10 times. Next game i.e 31st game will be between Alyssa and Bill and Bill wins it.

So total=5+10+1.

9 Helpful 0 Interesting 0 Brilliant 0 Confused

Just expanding on this. A proof that begins with an assumption is not a valid proof unless either (1) it is an indirect proof that proves the opposite of the assumption by logical contradiction or (2) the assumption is proved to be either necessary or irrelevant to the rest of the argument. In this case, assuming that Clayton never wins is logically allowable because the outcome of any games that he wins is irrelevant to the problem. Suppose, alternatively, that Clayton wins 1 game, or 5 games, or even 500 games. These would all be games between Clayton and Alyssa or Clayton and Bill, which Alyssa and Bill lose. Since we are only interested in the games Alyssa and Bill win, these games are all irrelevant. So we can assume Clayton wins any number of games and it will not affect the outcome for this problem.

Ed Rozmiarek - 3 years, 7 months ago

Log in to reply

Thank you for explaining that.

Robert Rojas - 3 years, 7 months ago
Jose Jimenez
Nov 6, 2017

My solution is somewhat similar to Patrick's comment, but I think it deserves a graphical explanation:

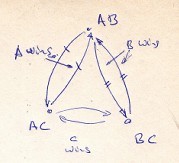
We start in the upper situation (A against B). AB in the figure. If A wins, we move to AC (A against C). If B wins we move to BC (B against C).

Then the match continues moving across these 3 states AB, AC, BC.

Every time A wins, the movement is along lines marked /

Every time B wins, the movement is always along lines marked by // .

Since A wins 10 times, we move 10 times along / lines. B wins 21 times, therefore we move 21 along // lines. (the number of movements along the not marked lines -C wins- is indifferent). There are many ways to make those 31 movements, but they always result in AB being visited 15 times, plus the original.

For example: one extreme possibility is 10 movements along the AB-AC loop and then 21 movements along AB-BC. Other possibilities include movements along the non marked lines, including circular moves AB-BC-AC-AB. However, it is easy to realise that, regardless of the path finally followed, AB is visited 15 times. That, counting the initial game leaves 16 total AB games.

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Emmanuel David
Nov 11, 2017

I just imagined the case where Bill won the first 21 games and Alyssa won the next 10 games.

The Sequence is as follows:

B A
B C
B A
B C
B A
B C
B A
B C
B A
B C
B A
B C
B A
B C
B A
B C
B A
B C
B A
B C
B A
A C
A B
A C
A B
A C
A B
A C
A B
A C
A B
0 Helpful 0 Interesting 0 Brilliant 0 Confused
Marin Badurina
Nov 10, 2017

This is a simple solution, but felt more like a lucky guess:

Every time someone wins, they get another opponent. There are 2 opponents. It can't be "rock-paper-scissors" because the numbers of wins are different.

Then I went for multiplying the wins by 1 2 \frac{1}{2} and adding the results together. (2 being the number of contestents for the current winner.)

I got 10 2 \frac{10}{2} + 21 2 \frac{21}{2} =15.5 I needed to know Bill's first matchup to round it up or down. It was Alyssa, so I rounded to 16.

Now, I know this ain't the correct way to do it, but I want to know why it worked. And why it wouldn't. I guess it only works for 3 people total. Please, comment. I'm trying to learn math :P

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Kanad Pardeshi
Nov 9, 2017

Let A A represent Alice, B B represent Bob, and C C represent Clayton. When a player X X wins against a player Y Y , let us represent it as \((X,Y)\. Note that whenever A or B win against C, they must play against each other. Also, as A and B play one game in the beginning, the number of games they play between them is one more than the total number of times they have won against C.

\((A,C)+(B,C)+1=(A,B)+(B,A)...(1)\)

( A , C ) + ( A , B ) = 10... ( 2 ) (A,C)+(A,B)=10...(2)

( B , C ) + ( B , A ) = 21... ( 3 ) (B,C)+(B,A)=21...(3)

( 2 ) + ( 3 ) : (2)+(3):

( A , C ) + ( A , B ) + ( B , C ) + ( B , A ) = 31... ( 4 ) (A,C)+(A,B)+ (B,C)+(B,A)=31...(4)

We add ( A , B ) + ( A , B ) (A,B)+(A,B) to both sides in ( 1 ) . (1).

Then,

( A , B ) + ( B , A ) + ( A , C ) + ( B , C ) + 1 = 2 ( A , B ) + 2 ( B , A ) = 32. (A,B)+(B,A)+(A,C)+(B,C)+1=2(A,B)+2(B,A)=32.

Therefore,

( A , B ) + ( B , A ) = 16. (A,B)+(B,A)=16.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

The first game they played was against eachother, which results in the first win for either alyssia or Bill. For them to meet again Any one of Bill and alyssia has to win a match. So win nr 2 Will NOT be a match between alyssia and bill. After win nr2 they Will meet and one of them has to win so win nr3 is a match between them. And this goes on and on. The only time they win and play against eachother is when the win will be a odd win (2n+1). They have together 31 wins and from 1-31 there are 16 odd Numbers (1,3,5,7,8..31). Therefore they met eachother 16 Times.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...