Christmas Streak 50/88: Geometry + Number Theory
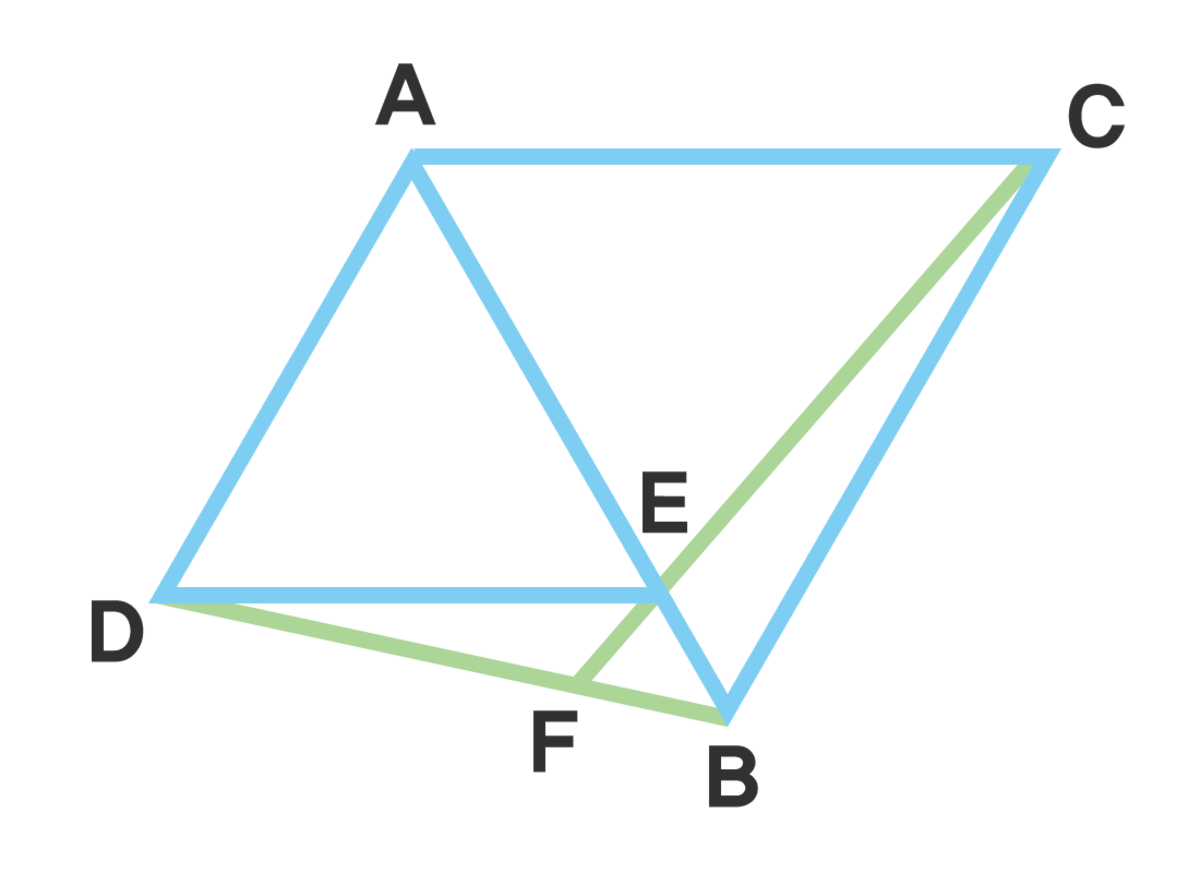 Image not drawn to scale.
Image not drawn to scale.
and are equilateral triangles, satisfying and
Given that are positive integers larger than 1, the area of is for some coprime integers and and a square-free integer
Find the value of
This problem is a part of <Christmas Streak 2017> series .
The answer is 198770.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Geometry
The congruence of △ A D B and △ A E C is trivial. ⇒ ∠ A B D = ∠ A C E .
Since ∠ A E C = ∠ F E B , we see that △ A E C ∼ △ F E B .
Therefore B E : C E = F E : A E , leading to B E × A E = C E × F E = 6 3 0 .
We know that B E = x 2 + y 2 + 2 − ( 2 x + y 2 + 1 ) = x 2 − 2 x + 1 = ( x − 1 ) 2 , and A E = 2 x + y 2 + 1 .
Number Theory
( x − 1 ) 2 ( 2 x + y 2 + 1 ) = 6 3 0 = 2 × 3 2 × 5 × 7
Since ( x − 1 ) 2 is a square while also being a divisor of 630, it's either ( x − 1 ) 2 = 1 or ( x − 1 ) 2 = 9 .
x = 2 , y = 2 5 or x = 4 , y = 6 1 .
The latter is impossible, so we know that x = 2 and y = 2 5 .
Geometry
Then A D = 6 3 0 , and A B = 6 3 1 .
So we know that △ A D B = 2 1 × 6 3 0 × 6 3 1 × 2 3 = 2 1 9 8 7 6 5 3 .
Therefore, a + b + c = 1 9 8 7 7 0 .