Christmas Streak 59/88: 2018 CSAT (Korean SAT) #21 of Liberal Arts

Algebra Level 5

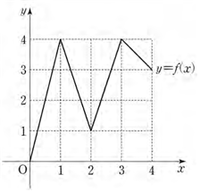
As shown on the right, the graph of $f(x)$ , a function defined in the interval $[0,4]$ , is equivalent to sequentially connecting the points $(0, 0)$ , $(1,4)$ , $(2,1)$ , $(3,4)$ , $(4, 3)$ each with a straight line segment.

How many sets $X=\{a,b\}$ are there that satisfy the below condition? $(0\le a<b\le 4)$

There exists a function $g:X\to X$ where $g(x)=f(f(x))$ and $f(a)=g(a)$ and $f(b)=g(b).$

This problem is a part of <Christmas Streak 2017> series .

17 11 15 18 12 13 16 14

1 solution

Boi (보이)
Dec 1, 2017

Since $g(x)=f(f(x))$ and $g(x)=f(x),$ we know that $f(x)=f(f(x))$ for $x=a,~b.$

If $f(a)=a,$ then $f(b)=a,~b.$ If $f(b)=b,$ then $f(a)=a,~b.$

But if $f(a)=b,$ then $f(b)=b.$ . If $f(b)=a,$ then $f(a)=a.$

From this we notice that there are two cases:

$i)~f(a)=a,~f(b)=b$

Then the number of sets $X$ is equivalent to the number of methods of choosing two points from the four intersections of $y=f(x)$ and $y=x.$

$_4\mathrm{C}_2 = 6.$

$ii)~f(a)=f(b)=a~\text{or}~f(a)=f(b)=b$

Let the four intersections of $y=f(x)$ and $y=x$ be $\mathrm{A}_0,~\mathrm{B}_0,~\mathrm{C}_0,~\mathrm{D}_0.$

Then draw lines perpendicular to the $y$ -axis from each point and find the intersections between each of them and the graph of $y=f(x).$

Let $A=\{\mathrm{A}_0,~\mathrm{A}_1,~\mathrm{A}_2,~\mathrm{A}_3\},~B=\{\mathrm{B}_0,~\mathrm{B}_1,~\mathrm{B}_2\},~C=\{\mathrm{C}_0,~\mathrm{C}_1,~\mathrm{C}_2\},~D=\{\mathrm{D}_0\}$ be the sets of equal $y$ -coordinates of those intersections.

Pick one of those sets, and choose two among the elements.

But since at least one of $(a,~g(a))$ and $(b,~g(b))$ must be on $y=x,$ we must pick the first element of the set.

Therefore there are $3+2+2+0=7$ ways of doing this.

From above, the total number of cases is $6+7=\boxed{13}.$

(Sorry for the crap explanation.)

I made a counting error and got this one wrong... great problem!

Our givens are g(x) = f(f(x)) and g(x) = f(x) for all x in X. Putting these together we find f(f(x)) = f(x), which shows that f(x) = g(x) has to be a fixpoint of f. Drawing the line y = x through the given graph and finding the intersections shows us that there are four fixpoints: 0, 7/4, 5/2, and 7/2. (It is not necessary to find these values —I called them p, q, r, and s— but I don't know how to attach an image!)

One possibility, then, is that X consists of two of these fixpoints. There are (4 choose 2) = 6 such options: {0, 7/4}, {0, 5/2}, {0, 7/2}, {7/4, 5/2}, {7/4, 7/2}, and {5/2, 7/2}.

The other possibility is that X contains one of these fixpoints x, and some non-fixpoint w such that f(w) = x. So for each fixpoint we need to find its preimages. (We can do this by drawing horizontal lines through the above intersections.)

0 has no other preimages, so there are no possibilities for a set {0, w}, where f(w) = 0 but w ≠ 0.

7/4 has two other preimages, so there are 2 possibilities for a set {7/4, w}, where f(w) = 7/4 but w ≠ 7/4

Similarly, there are 2 such possibilities for {5/2, w} and 3 for {7/2, w}.

In total, we find 6 + (0 + 2 + 2 + 3) possibilities for X.

Jeremy Weissmann - 3 years, 6 months ago

it is frustrating. i made a small mistake.

Srikanth Tupurani - 1 year, 9 months ago

Christmas Streak 59/88: 2018 CSAT (Korean SAT) #21 of Liberal Arts

1 solution

0 pending reports