Christmas Streak 68/88: Where is wrong? #1
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
It can't be said that a + b = a + b holds for every reals a and b .
So the wrong part is 9 + 1 6 = 9 + 1 6 .
In-depth explanation:
Let's then say a + b = a + b for all reals a and b .
Then it must be the case that a + b = ( a + b ) 2 = a + b + 2 a b .
This implies that a b = 0 for all reals, which is clearly false.
Therefore, for a + b = a + b to hold, at least one of a and b is 0 .
Why can’t it be said so?
@H.M. 유 Nice Drawings
Can you tell me -where do you draw and how to post my drawing or some figure on brilliant?
Log in to reply
I drew them on Adobe Photoshop, and posting images to brilliant is easy - you just need to drag it to the top bar.
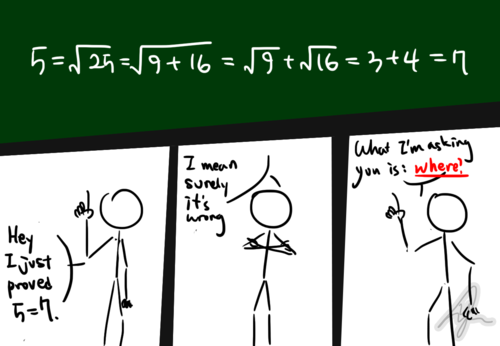
Obviously, √ a b = √ a √ b , this is an identity, but √ a + b is not √ a + √ b . It is a common mistake made in algebra.