Christmas Streak 74/88: Geometry Rush #4

Only if b² >ac can we have the figure as shown. Thus since 21²>7x14 & 14²>21x7 but 7²<14x21, we have only two possibilities so that: a=7,b=14,c=21, x=ac(a+2b+c)/(b^2-ac) =168 or a=7,b=21,c=14 and x=18.

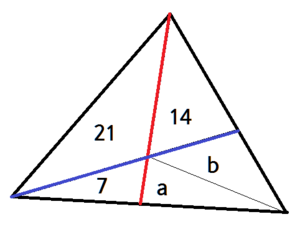
Consider this case, where $21$ is the area of the sub-triangle not adjacent to the quadrilateral.

Think about the ratio between the two parts of the red line. It can be expressed in two ways:

$7:21$ and $a:14+b.$

Since these two ratios must be equal, $1:3=a:14+b.$ Inners together, and outers together.

$\color{#D61F06}3a=b+14.$

Then think again about the ratio between the two parts of the blue line.

Because of the same reason, $3:2=a+7:b~\Leftrightarrow~\color{#3D99F6}3b=2a+14.$

Subtract red from blue side by side to get $3b-3a=2a-b~\Leftrightarrow~b=\dfrac{5}{4}a.$

Now substitute this to red. $\longrightarrow~3a=\dfrac{5}{4}a+14~\Leftrightarrow~\dfrac{7}{4}a=14~\Leftrightarrow~a=8.$

$b=\dfrac{5}{4}a=10.$

Therefore the quadrilateral has an area of $8+10=18.$

---

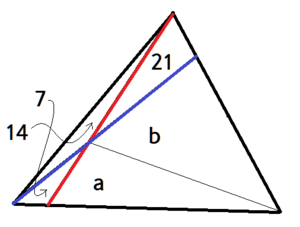
Let's fast-forward a little bit.

${\color{#D61F06}1:2=a:b+21~\Leftrightarrow~2a=b+21};~{\color{#3D99F6}2:3=a+7:b~\Leftrightarrow~2b=3a+21}.$

Now subtract red from blue side by side to get $b=\dfrac{5}{3}a.$

Substitute to red to get $a=63$ and subsequently $b=105.$

Yes, very huge.

The area is $63+105=168.$

.

.

---

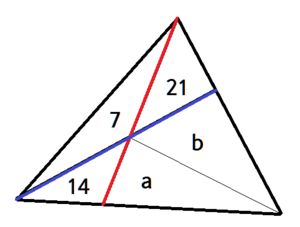
See this diagram? Isn't it a bit off compared to the other two?

Yeah, conclusions first, this case is not possible.

${\color{#D61F06}a=2b+42};~{\color{#3D99F6}b=3a+42}.$

Red - Blue: $b-a=3a-2b~\Leftrightarrow~b=\dfrac{4}{3}a.$

Substitute to red to get $a=\dfrac{8}{3}a+42~\Leftrightarrow~\dfrac{5}{3}a=-42.$

Ah. We now see why. The areas happen to be negative. (which kinda means ${\rm P}$ is in the exterior)

.

---

From above, the only possible areas for the quadrilateral are $18$ and $168,$ whose sum is equal to $18+168=\boxed{186}.$