Christmas Streak 77/88: Geometry Rush #7
Image seriously not drawn to scale.
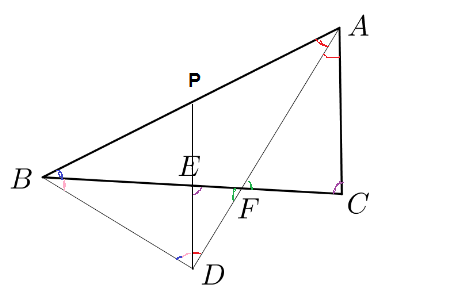
In a triangle A B C shown on the right, let D be the foot of perpendicular from B to the bisector of ∠ B A C .
Also, pick a point E on B C such that D E / / A C .
Given that D E = 5 , A B = 2 5 , E F = 4 , find the length of the perimeter of △ A B C .
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
" we figure out that AC=15." Can You please Explain how? Thanks.
from bisector theorem and simliarity between △ A C F and △ D E F B F A B = B F 2 5 = C F A C = E F D E = 4 5 ∴ B F = 2 0
since △ B D A is a triangle rectangle and ∠ A D P = ∠ D A P thus P is the midpoint and again by similiarity △ B E P △ B C A 2 B E = B C = 3 2
by triangle simliarity F E F C = 4 1 2 = E D A C = 5 A C = 3 ∴ A C = 1 5 so answer is 1 5 + 2 5 + 3 2 = 7 2
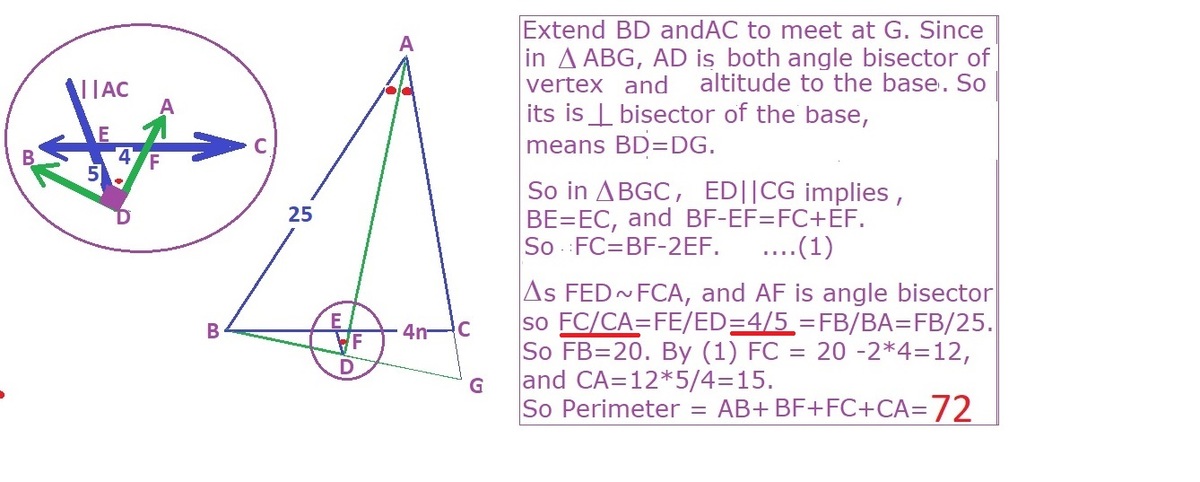
Oops, my hand slipped and I accidentally conveniently extended B D and A C .
Since A D bisects ∠ B A C , we note that B D = D P , and thus 2 D E = C P = 1 0 . ( △ B D E ∼ △ B P C )
Then since A P = A B = 2 5 , we figure out that A C = A P − C P = 1 5 .
△ D E F ∼ △ A C F . So C F = 3 E F = 1 2 .
Then B C = 2 C E = 3 2 .
Therefore, the length of the perimeter of △ A B C is A B + B C + C A = 2 5 + 3 2 + 1 5 = 7 2 .