Chromatic polynomial - 2
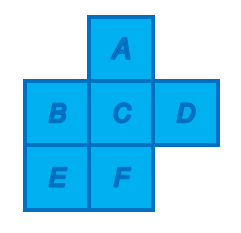
Suppose we want to color the six regions using red, yellow and blue so that no two regions sharing the same edge have the same color.
How many possible ways to color the regions?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
It might be an unnecessary step, but I represent the diagram n a graph. The connection between two vertices means they are adjacent.
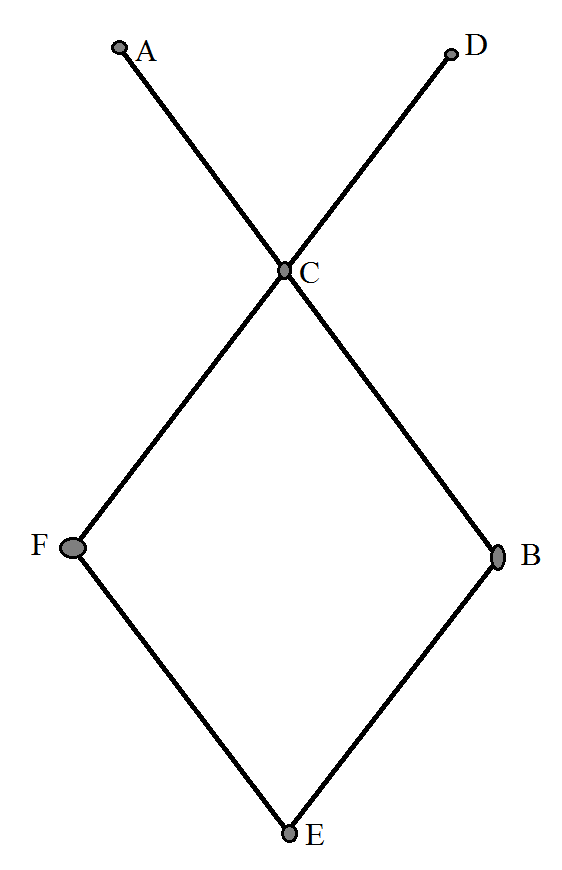
the vertice that has the highest degree is C. That's why it's a good idea to begin with this letter. You have 3 options: red, yellow and blue. A and D are connected only with C, so their color depends only on our first choice. each can have 2 colors (since one was already chosen to be at C). That already gives us 3 ⋅ 2 ⋅ 2 = 1 2 possibilities. Then, we have to choose B and F. Without loss of Generality, label C's color as a and the other 2 possible colors b and c .
We can have B with b and F with b . In such case, E can either be a or c If B is b and F is c , E can only be a If B is c and F is b , E can only be a Finally, if B is c and F is c , E can either be a or b
In this last step we have 2 + 1 + 1 + 2 = 6 possibilities for the colors of B, E and F. Multiplying by the possibilities of the other regions: 6 ⋅ 1 2 = 7 2 possible ways
7 2
The chromatic polynomial will be x ( x − 1 ) 4 ( x − 2 ) if we start with highest degree vertex .So here putting x = 3 I am getting answer as 4 8 . Where I am making mistake ?
Each digit represents the number of color choices we have for that box, starting at C .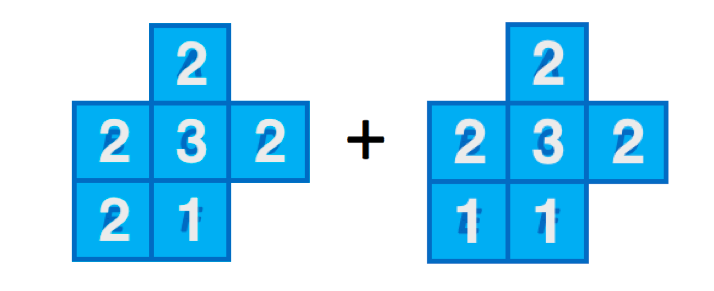 The tricky part is seeing that there are two separate cases:
B
=
F
(first image), which allows two choices for
E
, and
B
=
F
(2nd image), leaving just a single choice for
E
.
The tricky part is seeing that there are two separate cases:
B
=
F
(first image), which allows two choices for
E
, and
B
=
F
(2nd image), leaving just a single choice for
E
.
The total number of choices we have is 2 4 ⋅ 3 + 2 3 ⋅ 3 = 7 2
If we have a choice of n colors, we can generalize the result with the following polynomial:
C ( n ) = n ( n − 1 ) 4 + n ( n − 1 ) 3 ( n − 2 ) 2 ⟹ C ( n ) = n ( n − 1 ) 3 ( n 2 − 3 n + 3 )