Chromatic Polynomial - 3
Probability
Level
4
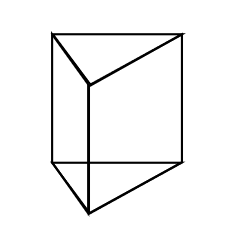
How many ways are there of coloring the triangular prism's vertices using 4 distinct colors so that no two adjacent vertices share the same color ?
240
264
288
168
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Stand the figure as in the picture.
Use markers A to D before choosing colours. Use markers A, B and C for the top 3 vertices.
You then may use A, B and C for the bottom three vertices in 2 ways. Each of the combinations ABD, ACD, and BCD can be used for the bottom vertices in 3 ways. Making 11 ways total. Now A B and C can be replaced with a colour each in 4x3x2 = 24 ways. So, in total, there are 24 x 11 = 264 colour schemes.