How Is A Chord Related To The Radius?

Geometry Level 2

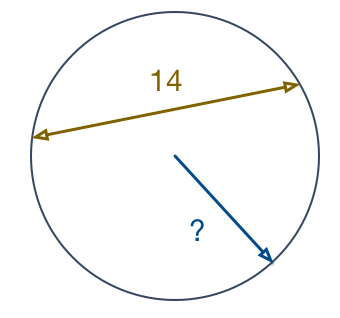
Given that a circle has a chord of length 14 cm, what can we conclude about the radius of this circle?

Cannot be determined Greater than or equal to 7 cm Less than or equal to 7 cm Exactly equal to 7 cm

1 solution

Chung Kevin
Feb 25, 2016

From wiki - circles , we know that a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle.

In other words, the diameter is the longest chord of the circle.

Now, back to the question, we are given that a circle has a chord of length 14 cm.

This tells us that the diameter, $d$ has a minimum value of value 14 cm, or $d \geq 14$ .

And because $\text{diameter } = 2 \times \text{ radius}$ , or simply $d = 2r$ , we have $2r \geq 14$ or $r \geq 7$ .

This tells us that the minimum radius of the circle is 7cm, and thus the desired answer:

$\text{The radius of this circle is } \boxed{\text{greater than or equal to 7 cm} }.$

The correct answer, if we rely on the pucture, is greater than 7: in fact, for how it is shown, the brown chord doesn't pass from the center, hence it can't be the diamater and therefore we have d = 2r > 14; if we instead ignore the picture and consider any possible chord to be 14 (diamater included) we have d = 2r >= 14, yielding the answer greater than or equal to 7. It should be specified whether we have to consider the image or not

Niccolò Gentile - 5 years, 3 months ago

Thanks. I've edited the options for clarity.

In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “dot dot dot” menu in the lower right corner. This will notify the problem creator who can fix the issues.

Calvin Lin Staff - 5 years, 3 months ago

Now the problem is not interesting, because part of the problem is exactly to determine that a diameter is also a chord of the circle. Better edit would be to remove the image.

Ivan Koswara - 5 years, 3 months ago

Yeah, you're right!

Salman Dahir Salman - 5 years, 3 months ago

The words in the problem don't refer to the image at all, so the image is to be ignored.

Ivan Koswara - 5 years, 3 months ago

Then the image should not be there is it is not part of the question. It should have only been the words.

Ian Turnbull - 5 years, 3 months ago

Let chord be AB and cenre of circle be O.

OA=OB=r.

In triangle ∆ABC,

angle OAB=angle OBA = x and

angle AOB = y.

2x+y=π so, y = π-2x .

By sine rule,

sin(x)/r = sin(y)/ 14

sin(x)/r = sin(π-2x)/14

sin(x)/r = sin (2x) /14

sin(x)/r = 2sin(x)cos(x)/14

1/r = cos(x)/7

r = 7 / cos(x)

as 0≤cos(x)≤1, r≥7

Ashwin Deshpande - 5 years, 3 months ago

Image should not be given then... Image was misleading us

Kumar Patchakanthala - 5 years, 3 months ago

Opps. I think diameter is not a chord of the circle.

Prasit Sarapee - 5 years, 3 months ago

The answer is wrong here. The LONGEST chord in a circle is the diameter. The problem does not state where the chord is in the circle. If we take it as the diameter, then the radius has to be 7. Now if the chord is NOT the diameter then the radius > 7. Thus, the question is worded incorrectly and not enough information to solve this problem. IF the problem stated that the chord was shown in the figure, then an answer can be determined. Since the figure is never mentioned in the question, the answer is "Cannot be determined". What this really is is a very good example of a poorly written question.

Donald Hammond - 5 years, 3 months ago

A chord in a circle has length 14. If it's the diameter, the radius is 7. If it isn't, the radius is greater than 7. Thus you can conclude that the radius is greater than or equal to 7. How can "cannot be determined" pop up?

Ivan Koswara - 5 years, 3 months ago

How Is A Chord Related To The Radius?

1 solution

0 pending reports