CIRCLE

Geometry Level 5

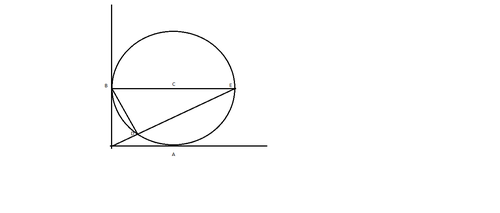A circle of unit radius touches positive x-axis and y-axis at A and B respectively. A variable line passing through origin intersects the circle in two points D and E. If the slope of the line is m and the area of triangle DEB is maximum. Find the value of arc(tan m) in degrees.

The answer is 30.

2 solutions

Vishal Choudhary
May 3, 2014

The equation of the circle is

(x-1)² + (y-1)² = 1 ....(1)

let the equation of the variable straight line be y=mx...........(2)

Solving (1) and (2),

we get

(1+m²)x² - 2x(1+m) +1=0

thus,

length DE=√(8m/(1+m²)

Area of the triangle DEB,A=1/2 DE * distance of B from DE

A² = 1/4.(8m/(1+m²))*1/(1-m²)=2m/(1+m²)²

A=√2m/(1+m²)

maximizing the area

dA/dm=(1-3m²)/√2m(1+m²)²=0

m=±1/√3

d²A/dm²<0 if m=1/√3

thus area is maximum at m=1/√3

arctan m = 30°

why the equation of the circle is like that? Is the circle supposed to have the center (1,1) ???

Nguyễn Phát - 6 years, 8 months ago

Dear Mr. Vishal Good Morning To You -

i used the same approach to solve this problem , which you have tried , but unfortunately , iam sorry to conclude that your solution is wrong because the squared distance from B to DE is 1/(1+m2) - plz recheck this !!!!!! hence this will cancel with analysing and the final result will be A = Sqrt( 2s ) , this will be maximum by substituting point ( 1,2) a point lying on the circle and satisfies its equation , consider this point (1,2 ) to be point E , THERFORE the slope m = 2 and Amax = sqrt (8) ,

arc ( tan m ) = arc ( tan 2 ) = 63.43 degrees thank you yours Aziz

Aziz Alasha - 5 years, 10 months ago

Chew-Seong Cheong
May 17, 2014

I used the same logic but I only considered the difference of x-coordinates of D and E which is proportional to the area A.

so you concluded that the difference of x-coordinates of D and E is proportional to the area A. by observing the determinant form of area of triangle,right?

Ashrene Roy - 6 years, 8 months ago

CIRCLE

The answer is 30.

2 solutions

0 pending reports