Two Kissing Semicircles

From the picture above, we knew that

$x=100-3r$

Through the Pythagorean theorem, we can obtain the following equation :

$50^2 + (x+r)^2 = (2r)^2$

Previously, we already know that $x=100-3r$ So,

$50^2 + (x+r)^2 = (2r)^2$

$50^2 + ([100-3r]+r)^2 = (2r)^2$

$50^2 + (100-2r)^2 = (2r)^2$

$2500+(10000 - 400 r + 4r^2) = 4r^2$

$12500 - 400r +4r^2 = 4r^2$

$12500 = 400 r$

$r = \frac{125}{4}$

$4r = 125$

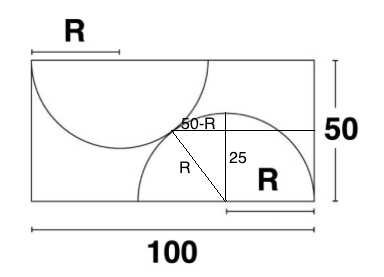
By symmetry, the intersection of the two circles must lies at the center of the rectangle. If we draw in lines to form this triangle, we can solve for R: $R^2=(50-R)^2+25^2$ $=>$ R=125/4 $=>$ 4R=125

We can use this relation to represent a circle.

$(x-h)^2+(y-i)^2=r^2$

Where h and i respectively denote the translation in the x and y directions on a Cartesian plane.

If we take the circle on the bottom for instance, it is plain to see that there is no vertical translation and the horizontal translation must be $100$ minus the radius.

Therefore, $h=100-r$ and $i=0$

From here we can sub in the point of intersection between the two circles $(50,25)$

$(50-(100-r))^2+(25-0)^2=r^2$

$2500+100r+r^2+625=r^2$

$3125+100r=0$

$r=31.25$

$4r=125$

*Thank you for the correction.

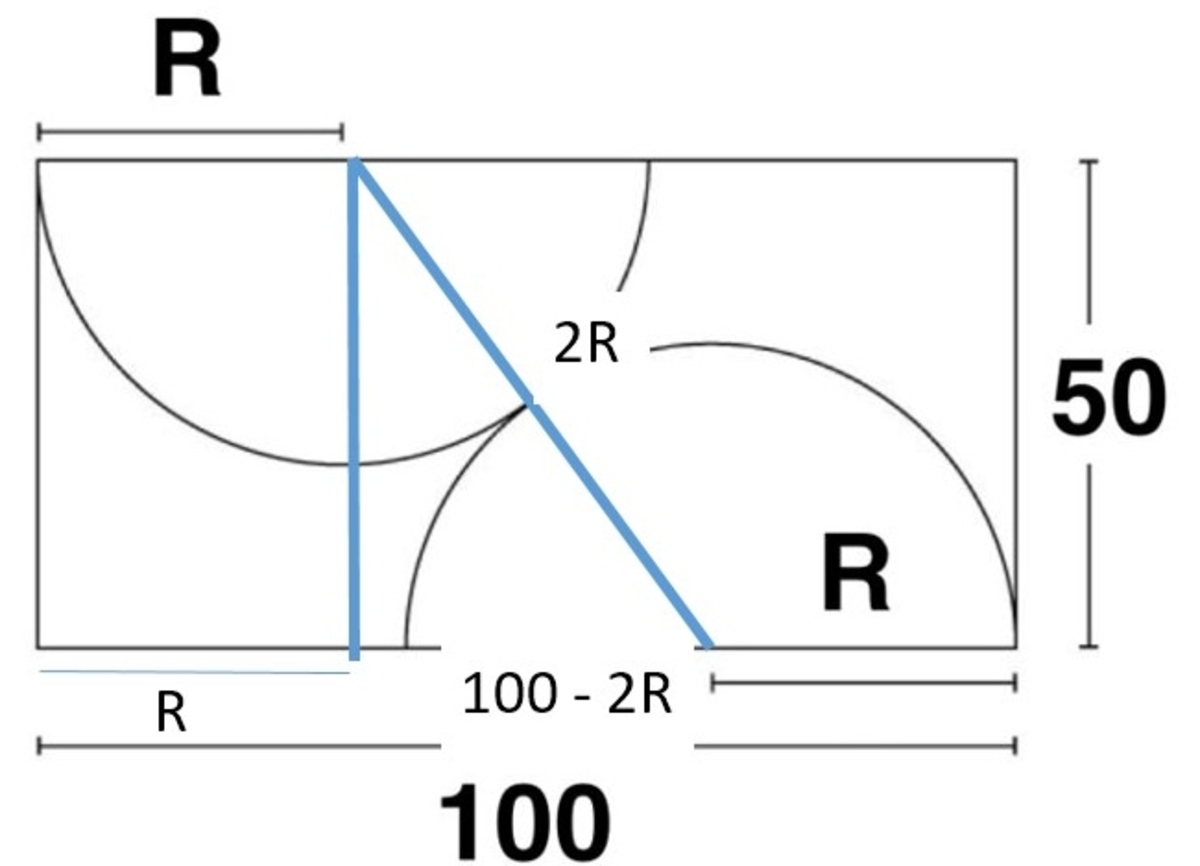
• $(2R)^2 - 50^2 = (100 - 2R)^2$
• $4R^2 - 2500 = 10000 - 400R + 4R^2$
• $400R = 12500$
• $4R = 125$

Let $x$ and $y$ be the horizontal and vertical distances respectively between the centre of a semicircle and the point of tangency. This gives us $2R + 2x = 100 \Rightarrow x = 50 - R \\ 2y = 50 \Rightarrow y = 25$ Squaring and combining these equations gives us $x^2 + y^2 = 2500 - 100R + R^2 + 625$ But by the Pythagorean theorem, $x^2 + y^2 = R^2$ , so $R^2 = 3125 - 100R + R^2 \\ \Rightarrow 100R = 3125 \\ \Rightarrow 4R = \boxed{125}.$

NICE SOLUTION Jayson.

it just solve this: $100-2r=\sqrt{((2r)^2-50^2)}$