Circle and square
The figure shows a square
A
B
C
D
such that
A
B
and
A
D
are tangents to a circle of radius 10. Points
C
and
E
are on circumference of the circle. Find the area of the triangle
A
B
E
.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
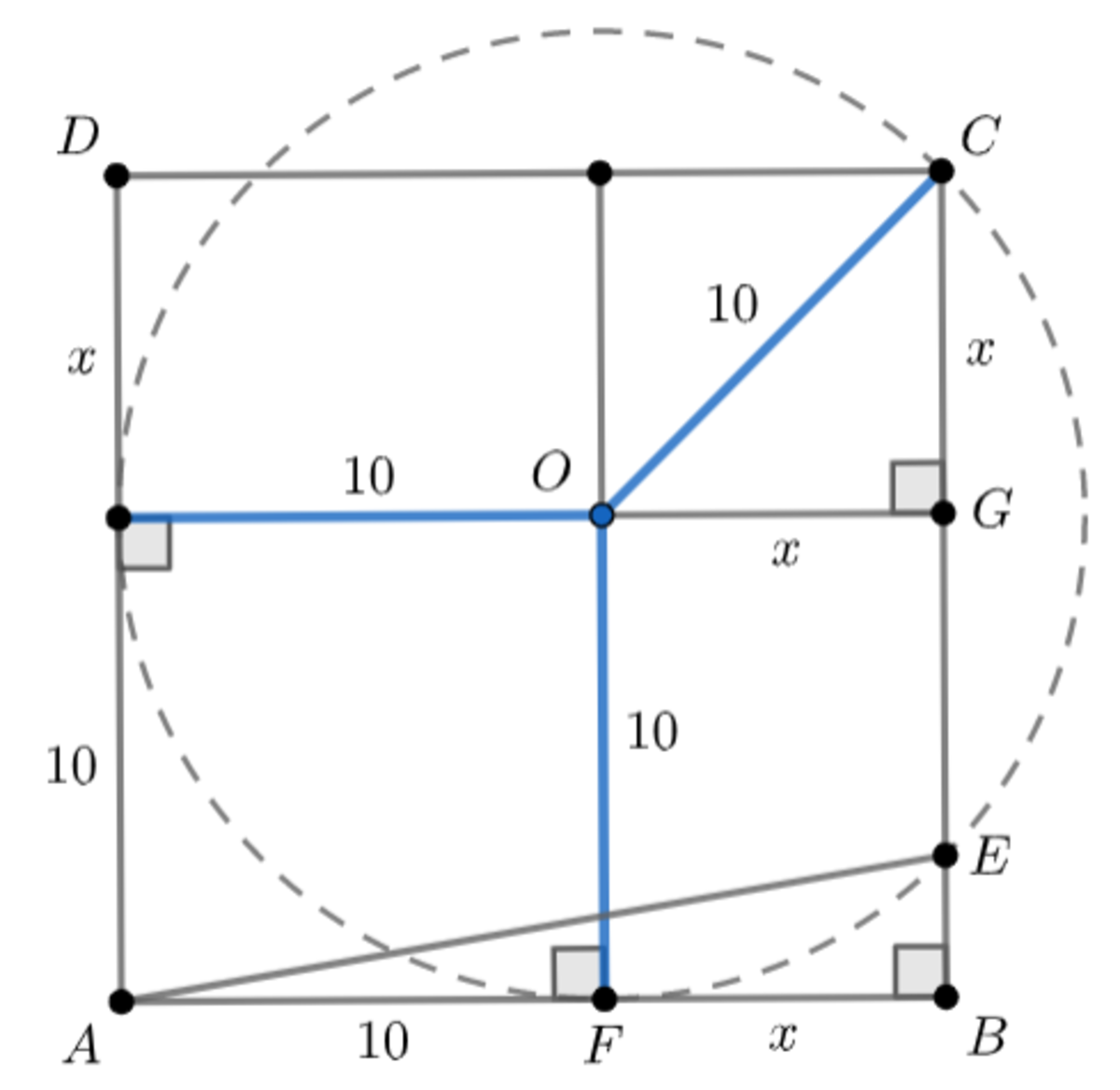 Since
B
F
is tangent to the circle, by
Tangent-Secant Theorem
,
B
F
2
x
2
⟹
B
E
=
B
E
⋅
B
C
=
B
E
⋅
(
1
0
+
x
)
=
1
0
+
x
x
2
In
△
C
O
G
,
O
C
2
1
0
2
⟹
x
=
C
G
2
+
G
C
2
=
x
2
+
x
2
=
5
0
Area of triangle
A
B
E
is,
Δ
=
2
1
⋅
A
B
⋅
B
E
=
2
1
⋅
(
1
0
+
x
)
⋅
1
0
+
x
x
2
=
2
x
2
=
2
5
Since
B
F
is tangent to the circle, by
Tangent-Secant Theorem
,
B
F
2
x
2
⟹
B
E
=
B
E
⋅
B
C
=
B
E
⋅
(
1
0
+
x
)
=
1
0
+
x
x
2
In
△
C
O
G
,
O
C
2
1
0
2
⟹
x
=
C
G
2
+
G
C
2
=
x
2
+
x
2
=
5
0
Area of triangle
A
B
E
is,
Δ
=
2
1
⋅
A
B
⋅
B
E
=
2
1
⋅
(
1
0
+
x
)
⋅
1
0
+
x
x
2
=
2
x
2
=
2
5
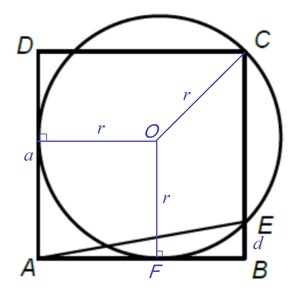
Let the center of the circle be O and its radius r , A B is tangent to the circle at F , and the side length of square A B C D be a . Then a = ( 1 + 2 1 ) r .
Let E B = d . Then by tangent-secant theorem , E B ⋅ B C = F B 2 ⟹ d a = ( a − r ) 2 , and the area of △ A B E .
A △ = 2 d a = 2 ( a − r ) 2 = 2 ( ( 1 + 2 1 − 1 ) r ) 2 = 4 r 2 = 4 1 0 2 = 2 5
for r = 1 0 .
Refer to the picture from the solution from Sathvik Acharya. Let L = AB = CB (they are equal since they are both sides of the same square). Construct radius OE (which, like all radii of the circle, has length 10). Then, by the hypotenuse-leg condition, we see triangles OCG and OEG are congruent. Therefore, GE has length x so that EB has length:
EB = L - 2*x. (equation 1)
But, by the Pythagorean Theorem, 2*x^2 = 100, so that x = sqrt(50)
However, we also note that 10 + x = DC = L, so that L = 10 + sqrt(50).
Thus, by substitution into equation 1, EB = 10 -sqrt(50)
We then note that:
Area (AEB) = (1/2) L (EB) = (1/2) (10 + sqrt(50)) (10 - sqrt(50)) = 50/2 = 25
https://www.desmos.com/calculator/gxdluoawec so you just notice the symmetry of a square and it can easily be made on desmos
sorry for the inaccraracy :y=\frac{2.929}{17.071}x