Circle and tangents
The tangent at ( 1 , 2 ) to the circle C 1 : x 2 + y 2 = 5 intersects the circle C 2 : x 2 + y 2 = 9 at A and B ; and the tangents at A and B on C 2 meet at P . If the coordinate of P is in the form ( b a , d c ) , where a , b are positive coprime integers, and c , d are positive coprime integers, then find a + b + c + d .
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
same method !!! just compare the tangent and chord of contact's equation ..
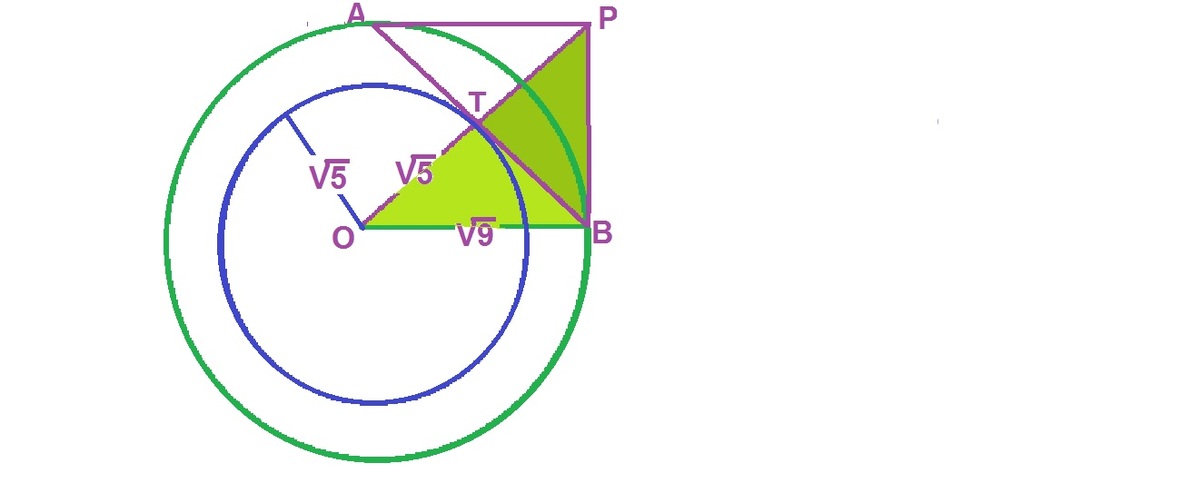
Let T=(1,2), and O=(0.0).
TO is perpendicular bisector of AB, the chord of
C
2
.
PAB also is an isosceles triangle. So PT is also perpendicular bisector of AB.
So O-T-P is a st. line.
B
O
=
9
,
T
O
=
5
.
.
So right tangles PTB ~ OTB.
∴
T
O
B
O
=
B
O
P
O
,
⟹
P
O
=
5
9
.
T
O
P
O
=
5
5
9
=
5
9
.
∴
P
=
(
5
9
∗
1
,
5
9
∗
2
)
=
(
5
9
,
5
1
8
)
=
(
b
a
,
d
c
)
.
a
+
b
+
c
+
d
=
9
+
5
+
1
8
+
5
=
3
7
Equation of tangent at P Is T = 0
So equation of tangent x+2y = 5 1...
Let point P is (x1,y1)
Equation of chord of contact from (x1,y1) to circle x^2 + y^2 = 9 is
xx1+yy1 = 9 2.....
1 and 2 are same equations so
1/x1 = 2/y1 = 5/9
as simple as that!