Circle and Triangle

Geometry Level 5

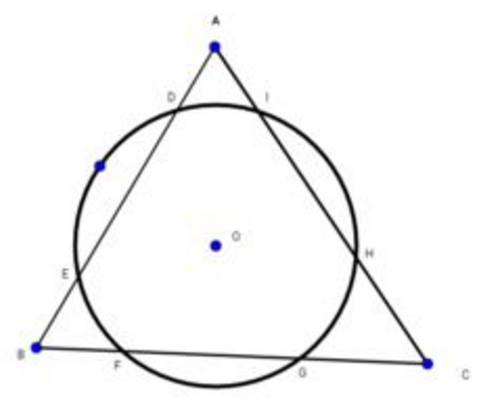
In the figure above, $AB,BC$ and $CA$ intersect the circle at the points $D,E,F,G,H$ and $I$ . Let $O$ denote the center of the circle such that $DE=FG=HI$ . If $\angle BAC =11^\circ$ . Find the measure of $\angle BOC$ in degrees.

The answer is 95.5.

1 solution

Niranjan Khanderia
May 23, 2016

Since chords of the circle DE=FG=HI, perpendiculars to them from center O must be equal. But that means O is at equal distances from the sides. So O is the incenter.
So OB and OC are angle bisectors of angles B and C.
B + C =180 - 11=169. So 1/2(B + C)=84.5.
Angle BOC=180 - 1/2(B + C) = $\color{#D61F06}{95.5^o}$

Circle and Triangle

The answer is 95.5.

1 solution

0 pending reports