Circle Areas #1: The Basics
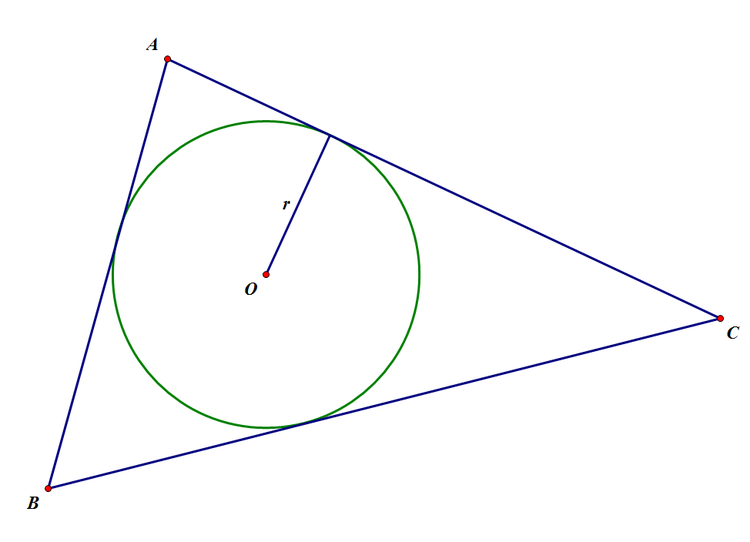 In the diagram above, Circle O is inscribed into Triangle ABC, where AB =
, AC =
, and BC =
. The area of Circle O can be written as
, where
is a constant. What is the value of
?
In the diagram above, Circle O is inscribed into Triangle ABC, where AB =
, AC =
, and BC =
. The area of Circle O can be written as
, where
is a constant. What is the value of
?
Note: Not to scale
This is part of the set Circles , made by Chris H.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you look closely, you'll see that { 3 , 4 , 5 } is a Pythagorean triple. Thus this triangle is right, i.e. 3 2 + 4 2 = 5 2 . The triangle has an area of 2 3 × 4 = 6 . The semiperimeter can be found as:
2 3 + 4 + 5 = 6
Using our formula for area, i.e. A = r s where r is the inradius and s is the semiperimeter, we can write:
6 = 6 r
Thus the inradius has length 1 . So the area is 1 2 π and the constant a = 1 2 = 1 .