Circle Areas #2: The Basics
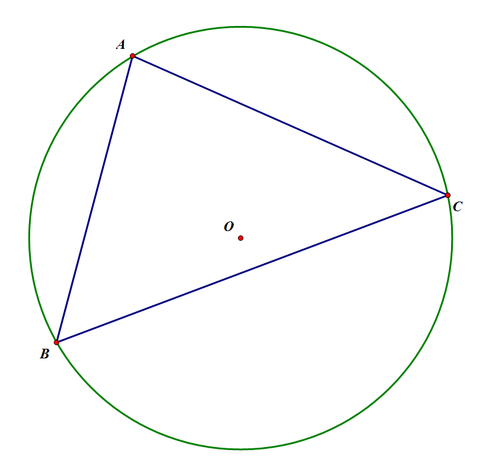 In the diagram above, Circle O is circumscribed about Triangle ABC, where AB=
, AC=
, and BC=
. The area of Circle O can be expressed as
, where
are constants, are positive integers, and share no common factors greater than 1. What is
?
In the diagram above, Circle O is circumscribed about Triangle ABC, where AB=
, AC=
, and BC=
. The area of Circle O can be expressed as
, where
are constants, are positive integers, and share no common factors greater than 1. What is
?
Note: Not to scale
This is part of the set Circles , made by Chris H.
The answer is 71.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Let R be the radius of the circumscribed circle. First we need to find the area of the triangle, denoted A . Using Heron's, this is
7 ( 1 ) ( 3 ) ( 3 )
Or 3 7 . The formula we need now is
R = 4 A a b c
where a , b , and c are the sides of the triangle. Plugging these in, R = 7 8 . Thus the area, or \ p i R 2 is 7 6 4 π . The desired answer is 6 4 + 7 = 7 1 .