This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I entered -6, needed that extra step to earn the credit for that exercise.
The solution is perfect. The way I understood is:
The big circle should have a r adius of CA + AD=
1
+
2
2
+
(
2
3
)
2
=
2
7
.
So the equation of the big circle is:-
(
x
+
2
)
2
+
(
y
+
2
3
)
2
=
(
2
7
)
2
.
⟹
x
2
+
4
x
+
4
+
y
2
+
3
y
+
4
9
=
4
4
9
.
∴
x
2
+
y
2
+
4
x
+
3
y
−
6
=
0
.
S
o
k
=
−
6
.
As the value of k increases, the radius of the circle centered at ( − 2 , − 2 3 ) decreases. When this circle touches the given circle which is centered at origin, the value of k can be obtained as follows,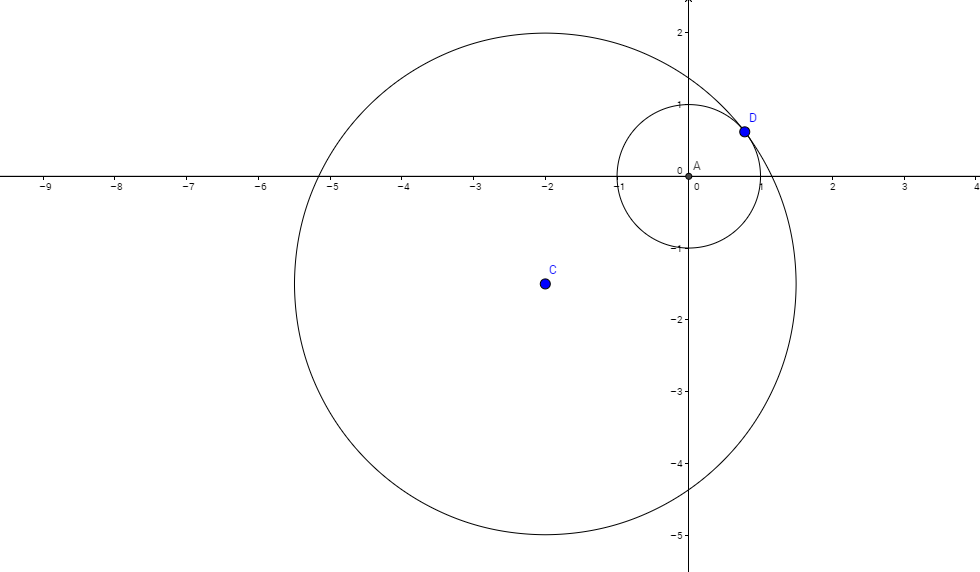
C D 2 2 + ( 2 3 ) 2 − k 4 2 5 − k k = A D + A C = 1 + 2 2 + ( 2 3 ) 2 = 2 7 = − 6
This is the case when the circles touch each other internally.
Hence, as per the condition required the maximum integer value of k is − 7 .