Circle buddies by themselves

Geometry Level 3

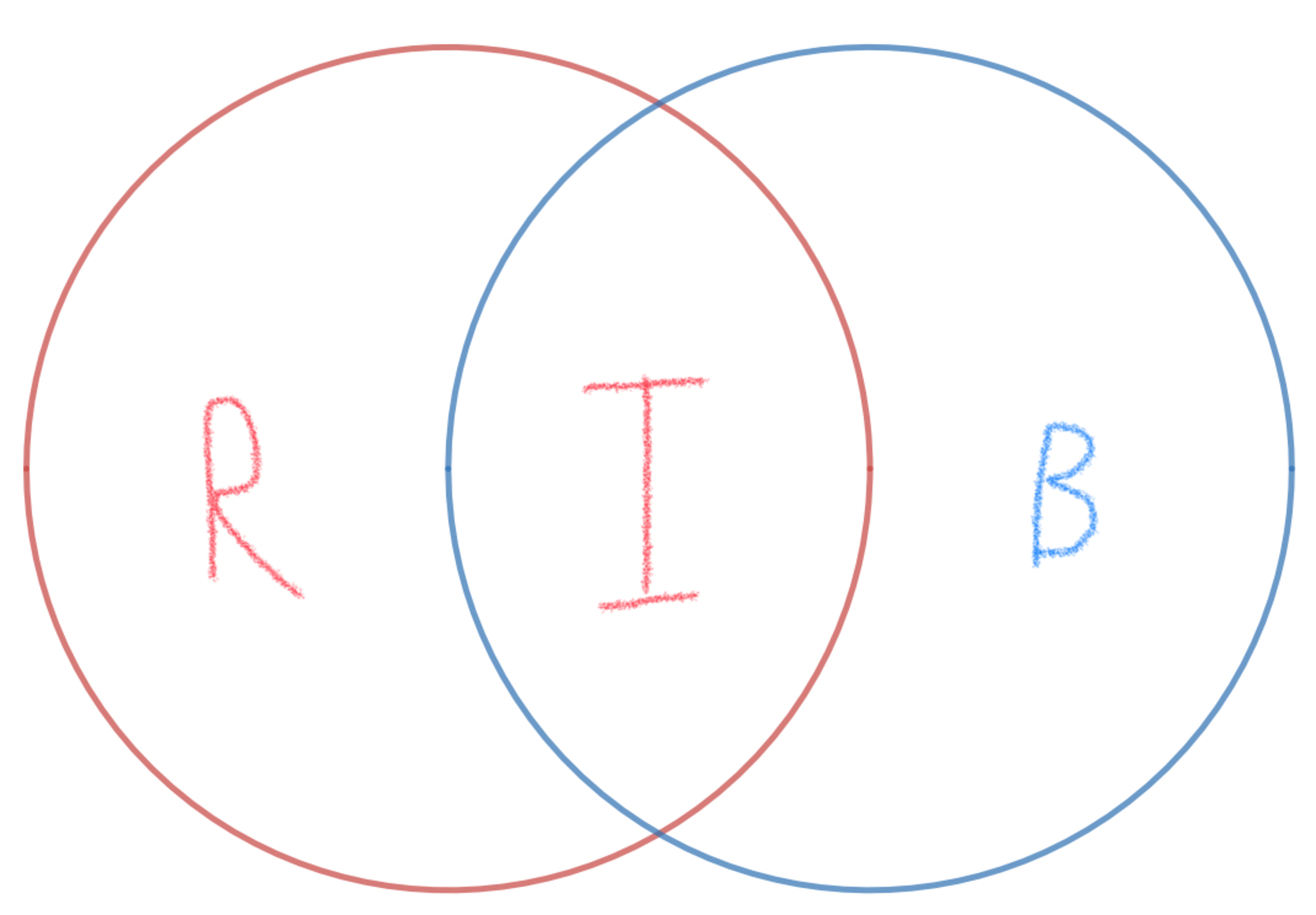
In the picture above, there are two circles, both with radius 1 1 . One circle passes through the other circle’s center (the red circle passes through the center of the blue circle, and vise versa).

The area of region I I , the region where the two circles intersect, can be expressed as:

a π + b c d \frac{a\pi +b\sqrt c}{d} ,

where a , b , c , d a,b,c,d are integers with c c square-free and d d minimized.

Evaluate 5 a + 5 b − 13 c + 6 d + c 2 5a +5b -13c +6d +c^2 .


The answer is 11.

Maximilian Million Kenney by Maximilian Million Kenney , 13

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The area of the common region between the two circles is 4 π − 3 3 6 \dfrac {4π-3\sqrt 3}{6}

So, a = 4 , b = − 3 , c = 3 , d = 6 ⟹ 5 a + 5 b − 13 c + 6 d + c 2 = 20 − 15 − 39 + 36 + 9 = 11 a=4,b=-3,c=3,d=6\implies 5a+5b-13c+6d+c^2=20-15-39+36+9=\boxed {11} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...