Circle buddies enclosed in a square
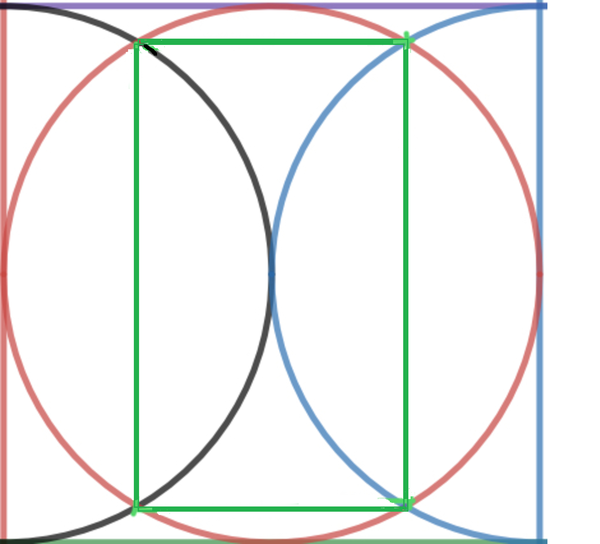
In the picture above, there is a square with side length 1 . A circle is inscribed in it, along with two semicircles on the sides.
A green rectangle is constructed by connecting the points of intersection of the two semicircles and the big circle.
The area of the green rectangle can be written as b a , where a and b are coprime positive integers and a doesn't have any perfect square factors other than 1 . Find the area of a square with side length b 3 − a 3 .
The answer is 1369.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note: All angles in this solution are in degrees, not radians.
We can make 2 equilateral triangles on each side of this rectangle with side length 2 1 as shown:
Phew! Triangles!
We can use the cosine rule here in order to find the left and right sides of this rectangle: ( Left/Right side ) 2 = 0 . 5 2 + 0 . 5 2 − 2 ( 0 . 5 ) ( 0 . 5 ) cos ( 1 2 0 ) = 4 3 Left/Right side = 4 3 = 2 3
We can see that the diagonal length inside the rectangle is 1 because it is the inner circle's diameter. Now we can use the Pythagorean Theorem to find the lower and upper sides: Lower/upper sides = 1 2 − ( 2 3 ) 2 = 4 1 = 2 1
Now we can calculate the area: Area = 2 1 ⋅ 2 3 = 4 3
We can see here that a = 3 and b = 4 . The side length of the square that we need to find the area of is 4 3 − 3 3 = 3 7 and the area is 3 7 2 = 1 3 6 9
Let the width of the green triangle be a and its height 2 b as shown in the figure. Note that the central red circle and the two semicircles have the same radius of 2 1 . The two semicircles touch at the center of the red circle. The center of the red circle and its two intersecting points with the semicircles form an equilateral triangle with side length a equal to the radius of the red circle which is 2 1 . That is a = 2 1 . The center of the red circle, one of its intersecting point with a semicirle and the point it touches the square also form an equilateral triangle with side length 2 1 . Then b = a sin 6 0 ∘ = 4 3 . Therefore the area of the green rectangle is A = 2 a b = 2 × 2 1 × 4 3 = 4 3 .
Therefore, ( b 3 − a 3 ) 2 = ( 4 3 − 3 2 ) 2 = ( 6 4 − 2 7 ) 2 = 3 7 2 = 1 3 6 9 .