Circle buddies in a rectangle
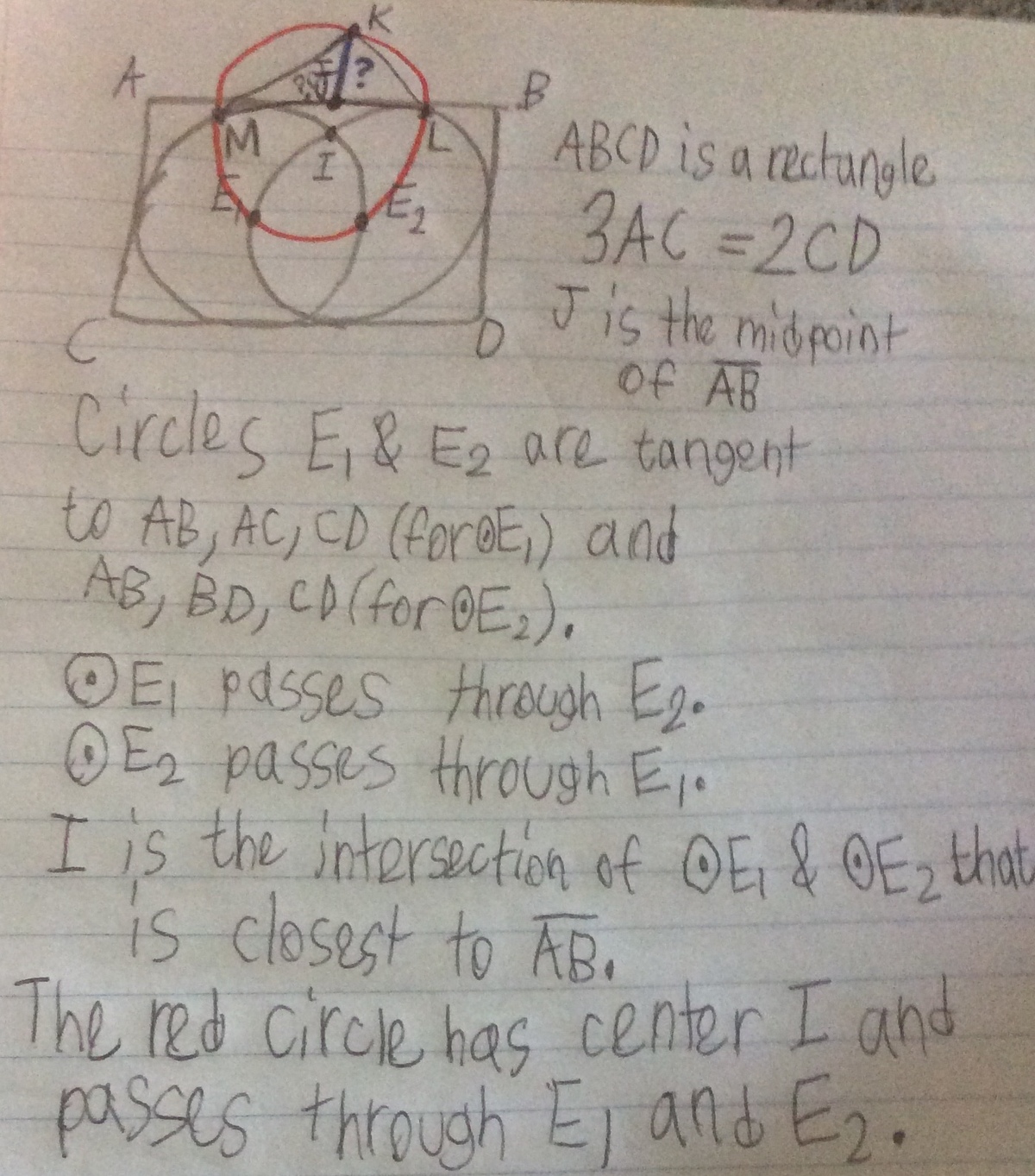
If is a point on O such that the distance from to is as small as possible, is the point at which O intersects O and is the point at which O intersects O , then:
Your goal is to find the area of quadrilateral .
The area can be expressed in the form , where and are coprime and has no prime perfect square factors.
Find the product of the coordinates of the uppermost point on a circle with equation .
In your solutions, assume .
O means .
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Problem requiring patience :)
Let the radius of each circle be r . Then the equation of E 1 , considering the origin of coordinates at C , is
( x − r ) 2 + ( y − r ) 2 = r 2
Equation of E 2 is
( x − 2 r ) 2 + ( y − r ) 2 = r 2
Solving we get the coordinates of I as
x I = 2 3 r , y I = 2 ( 2 + 3 ) r
Equation of red circle is
( x − 2 3 r ) 2 + ( y − 2 ( 2 + 3 ) r ) 2 = r 2
Solving this equation with the equation of E 1 we get the coordinates of M as
x M = 2 r , y M = 2 ( 2 + 3 ) r
Since ∣ J K ∣ is minimum, this line segment must be perpendicular to A B
So, coordinates of J are
x J = 2 3 r , y J = 2 r , and of K are
x K = 2 3 r , y K = 2 ( 4 + 3 ) r
So, area of △ J M K is
2 1 ∣ 2 r ( 2 4 + 3 r − 2 r ) + 2 3 r ( 2 r − 2 2 + 3 r ) + 2 3 r ( 2 2 + 3 r − 2 4 + 3 r ) ∣
= 4 r 2 3
It is given that r = 2 1 0 = 5
So, area of the triangle is 4 2 5 3
Since the triangles △ J M K and △ J L K have equal area, therefore area of the quadrilateral L J M K is twice the sum of △ J M K :
Area = 2 2 5 3
Hence X = 2 5 , Y = 3 , Z = 2
The equation of the given circle is
( x − 2 ) 2 + ( y − 3 ) 2 = 2 5 = 5 2
So the coordinates of the uppermost point of this circle are
x u = 2 , y u = 3 + 5 = 8 , and their product is x u y u = 2 × 8 = 1 6 .