Circle-ception: The next level
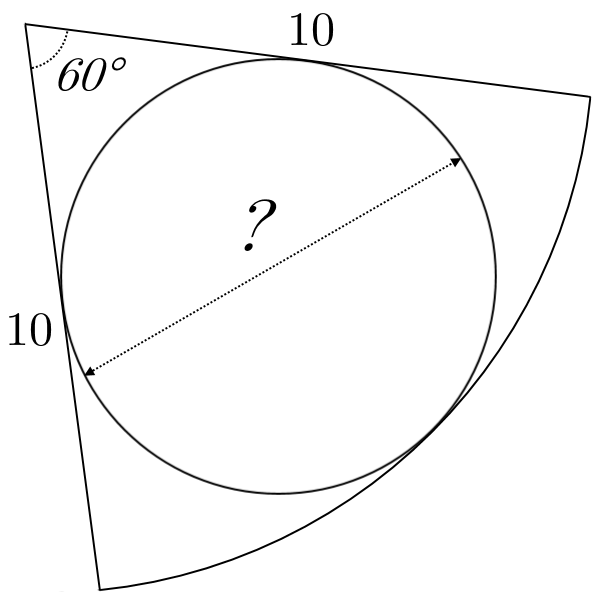 A sector of a circle of radius
and subtended angle
has a circle inscribed in it - its diameter can be written as
, where
and
are co-prime integers.
A sector of a circle of radius
and subtended angle
has a circle inscribed in it - its diameter can be written as
, where
and
are co-prime integers.
Find the value of
Part 1: Circle-ception .
The answer is 157.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This solution is similar to the one I posted for Circle-ception . This time, we bisect the 60° angle to form a right triangle with one leg x and hypotenuse 1 0 − x , where x is the radius of the incircle.
Using the sine rule, sin 3 0 x = sin 9 0 1 0 − x ⇒ 0 . 5 x = 1 1 0 − x ⇒ x = 5 − 2 x ⇒ 2 3 x = 5 ⇒ x = 3 1 0
Since x is the radius of the incircle, the diameter is 2 x = 3 2 0 , so a = 2 0 and b = 3 . ⌈ 2 0 + 3 2 0 2 × 3 2 ⌉ = ⌈ 2 3 3 6 0 0 ⌉ = ⌈ 1 5 6 + 2 3 1 2 ⌉ = 1 5 7