Circle chains
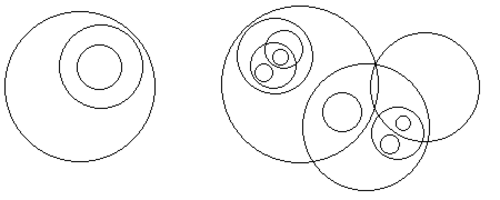 On a plane, a set of circles is called a
chain
if for any two circles in the set, one is completely inside the other. Note that any subset of a chain is also a chain.
On a plane, a set of circles is called a
chain
if for any two circles in the set, one is completely inside the other. Note that any subset of a chain is also a chain.
There are 100 (distinct) circles on the plane. Among any 10 of them, at least two circles form a chain. What is the minimum number of chains of size 10?
The answer is 154.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let a chain of 1 0 circles be called a bundle .
Note that if we have a chain of n circles, then the number of chains of size k in this chain is simply ( k n ) ; pick any k circles and they form a chain.
First, we claim that this number is at most 1 5 4 . Consider a collection of circles: 1 2 circles form a single chain, and the remaining 8 8 circles are divided into 8 chains of 1 1 circles each; these 9 chains are otherwise disjoint. By pigeonhole principle , there are 1 0 circles picked but only 9 chains present, so there are two circles that come from the same chain, and thus they form a chain, satisfying the condition of the problem. Afterwards, we can easily see that there are ( 1 0 1 2 ) = 6 6 bundles in the chain of size 1 2 , and ( 1 0 1 1 ) = 1 1 bundles in any chain of size 1 1 , for a total of 6 6 + 8 ⋅ 1 1 = 1 5 4 bundles. Finally, there is no other bundle; picking two circles from different chains won't make them a chain.
We will now prove that 1 5 4 is indeed the minimum (any such collection of circles must have at least 1 5 4 bundles).
Consider a partial order ( S , ≤ ) where S is the set of circles on the plane and ≤ is the relation completely contained in ; that is, if a ≤ b , then a is completely contained in b . It's straightforward to see that ≤ is a partial order:
Recall that if a ≤ b or b ≤ a , then a and b are said to be comparable ; otherwise, they are incomparable . A chain is thus an actual chain in order theory terminology: a set of elements such that any two of them are comparable. Also recall that an antichain (or independent set ) is a set of elements such that any two of them are incomparable.
The condition of the statement states that there is no antichain of size 1 0 , for if there is any, those 1 0 circles are pairwise incomparable, contradicting that some two circles should form a chain and thus comparable. Thus the size of the largest antichain is 9 . By Dilworth's theorem , this implies that it's possible to partition the circles into at most 9 (disjoint) chains; call these chains as big chains .
Suppose there is a big chain of 1 3 or more circles. Then there are at least ( 1 0 1 3 ) = 2 6 4 > 1 5 4 bundles, already passing our target.
Now suppose that there are a big chains of size 1 2 , b big chains of size 1 1 , and c big chains of size 1 0 or less. Also suppose there are B bundles in total. We have:
Note that by pigeonhole principle, there are 1 0 0 circles and 9 big chains, so at least one big chain has 1 2 circles. This means a ≥ 1 . Also,
1 0 0 − 1 2 a = 1 1 b + 1 0 c = b + 1 0 ( b + c ) ≤ b + 1 0 ( 9 − a )
Simplifying, this gives b ≥ 1 0 − 2 a . Also, we know that b ≥ 0 , so we have b ≥ max { 0 , 1 0 − 2 a } . Substituting to the last inequality, we have:
B ≥ ( 1 0 1 2 ) a + ( 1 0 1 1 ) b = 6 6 a + 1 1 b ≥ 6 6 a + 1 1 ⋅ max { 0 , 1 0 − 2 a } ≥ 6 6 a + 1 1 ⋅ ( 1 0 − 2 a ) = 1 1 0 + 4 4 a ≥ 1 1 0 + 4 4 ⋅ 1 = 1 5 4
This proves the claim, showing that 1 5 4 bundles is the minimum.