Circle covers square 2
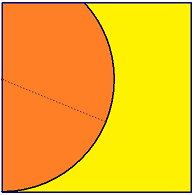
A circle covers precisely half of a unit square. The center of the circle is on one side of the square. One corner of the square is on the circle. Find the radius of the circle.
The answer is 0.596226128726910.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let O be the center of the circle, A be the corner of the square in the circle, C be the corner of the square that is on the circle, B be the other intersection of the square and the circle, r be the radius of the circle, and θ be ∠ A O B .
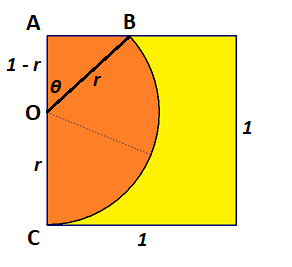
From △ A O B we find that A B = 2 r − 1 and θ = cos − 1 ( r 1 − r ) , so △ A O B has an area of A triangle = 2 1 ( 1 − r ) 2 r − 1 .
This means ∠ B O C = π − θ = π − cos − 1 ( r 1 − r ) , so sector B O C has an area of A sector = 2 π π − cos − 1 ( r 1 − r ) π r 2 .
The part of the circle covering the square is △ A O B and sector B O C , which must have a combined area of A triangle + A sector = 2 1 .
Therefore, 2 1 ( 1 − r ) 2 r − 1 + 2 π π − cos − 1 ( r 1 − r ) π r 2 = 2 1 , which solves numerically to r ≈ 0 . 5 9 6 2 .
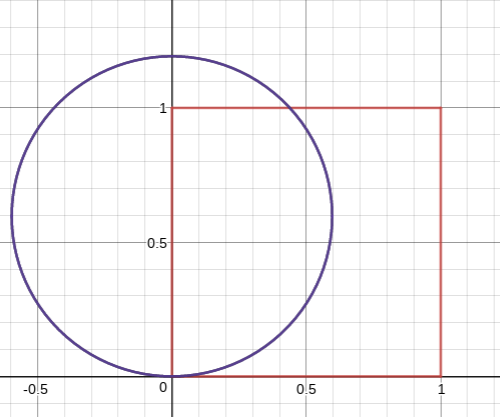
First, place the unit square on the coordinate plane, with vertices at
(
0
,
0
)
,
(
1
,
0
)
,
(
1
,
1
)
,
(
0
,
1
)
. Then, place the circle with the both point at
(
0
,
0
)
. The graph for this circle is
x
2
+
(
y
−
a
)
2
=
a
, where
a
is the radius of the circle. If the circle has a radius of
2
1
, the top of the circle will be at one of the vertices of the square, and the point furthest right on the circle hits the midpoint of the square. Because of the curve of the circle, this is obviously less than half of the square. So therefore
a
>
2
1
, and
a
>
4
1
. Then, take the integral from
1
to
0
, with respect to y, of the circle. Rearranging the equation of the circle we get
x
=
a
−
(
y
−
a
)
2
. In integral format, we get
∫
0
1
(
a
−
(
y
−
a
)
2
d
y
, and we want this to equal
2
1
, half of the area of the unit square. I tried various numbers on desmos, until I found that
a
=
0
.
3
5
5
4
8
5
5
9
6
5
7
7
, and so the radius is
a
=
0
.
5
9
6
2
2
6
1
2
8
7
2
7
.
2 ( π − θ ) r 2 Area of sector + 2 r 2 cos θ sin θ Area of triangle ( π − cos − 1 ( r 1 − r ) ) r 2 + ( 1 − r ) 2 r − 1 = 2 1 = 1 Note that cos θ = r 1 − r ⟹ θ = cos − 1 ( r 1 − r ) ⟹ sin θ = r r 2 − ( 1 − r ) 2 = r 2 r − 1
Solving it numerically, we have r ≈ 0 . 5 9 6 .