Circle cuts circle - (4)

Geometry Level 5

Two circles of radii one and two units respectively cut each other at an angle of 6 0 ∘ 60^\circ . If the length of the common chord of these two circles can be expressed in the form a b c \dfrac{a\sqrt{b}}{c} where b b is square free , find the value of a + b + c a+b+c .

This question is a part of this set (click here) . Follow me for more! :)


The answer is 30.

Nihar Mahajan by Nihar Mahajan , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions


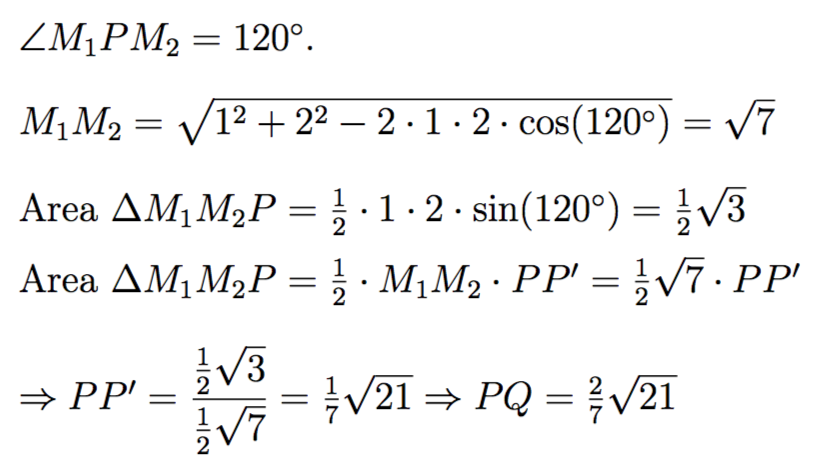
A p p l y i n g S i n L a w t o Δ A B C , A B S i n ( 60 − α ) = B C S i n ( α ) ⟹ 1 2 = S i n 60 ∗ C o s α − C o s 60 ∗ S i n α S i n α . S i m p l i f y i n g C o t α = 2 3 . ∴ S i n α = 21 7 . C o m m o n C h o r d = 2 ∗ B D = 2 ∗ A B S i n α = 2 21 7 . a + b + c = 2 + 21 + 7 = 30 Applying ~Sin~ Law ~to ~\Delta~ ABC , ~\dfrac{AB}{Sin(60-\alpha)} =\dfrac{BC}{Sin(\alpha)} \\ \implies ~\dfrac 1 2=\dfrac{Sin60*Cos\alpha - Cos60*Sin\alpha}{Sin\alpha}. \\ Simplifying ~ Cot\alpha=\dfrac 2 {\sqrt3}. ~~\therefore ~Sin\alpha=\dfrac {\sqrt {21}} 7.\\ Common~ Chord=2*BD=2*ABSin\alpha=2\dfrac {\sqrt {21}} 7.~~~~~~a+b+c=2+21+7=30

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...