Circle Cutting an Equilateral Triangle
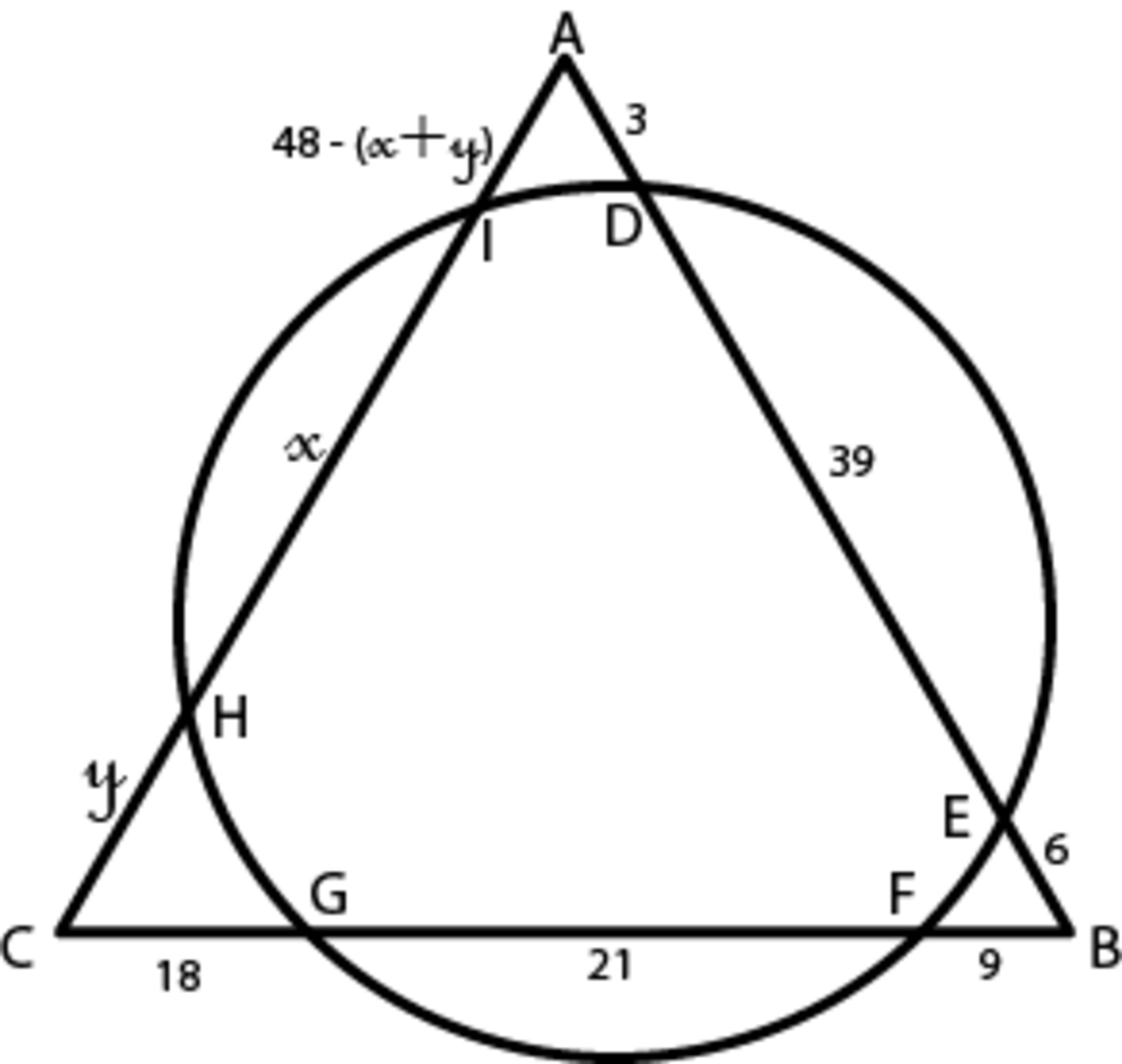
A circle Γ cuts the sides of a equilateral triangle A B C at 6 distinct points. Specifically, Γ intersects A B at points D and E such that A , D , E , B lie in order. Γ intersects B C at points F and G such that B , F , G , C lie in order. Γ intersects C A at points H and I such that C , H , I , A lie in order. If ∣ A D ∣ = 3 , ∣ D E ∣ = 3 9 , ∣ E B ∣ = 6 and ∣ F G ∣ = 2 1 , what is the value of ∣ H I ∣ 2 ?
Details and assumptions
∣ ⋅ ∣ notation denotes the straight line distance between points and not the arc length distance.
The answer is 792.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Common mistakes
- There are 2 solutions to a quadratic. You have to explain why you chose a particular root, or why the other one doesn't work.
Log in to reply
You'll get ∣ H I ∣ = ± 6 2 2 , directly!
By Power of Point with respect to point B , we have that B E ⋅ B D = B F ⋅ B G , so 6 ⋅ 4 5 = B F ( B F + 2 1 ) . It is easy to verify that the only positive solution is B F = 9 . Because △ A B C is equilateral, we have that A B = 3 + 3 9 + 6 = B C = 9 + 2 1 + G C , so the side length of △ A B C is 4 8 and G C = 1 8 .
Let A I = a , H I = b , and C H = c . By Power of Point with respect to points A and C , we obtain: a ( a + b ) = 3 ( 3 + 3 9 ) = 3 ( 4 2 ) = 1 2 6 and c ( b + c ) = 1 8 ( 1 8 + 2 1 ) = 1 8 ( 3 9 ) = 7 0 2 . Note that a + b + c = 4 8 , so we can rewrite the two equations as: a ( 4 8 − c ) = 1 2 6 and c ( 4 8 − a ) = 7 0 2 .
Expanding both, we obtain 4 8 a − a c = 1 2 6 and 4 8 c − a c = 7 0 2 . Subtracting the two equations and dividing by 4 8 , we obtain c − a = 1 2 , and so c = a + 1 2 and a = c − 1 2 .
Plugging in c = a + 1 2 into a ( 4 8 − c ) = 1 2 6 gives a ( 3 6 − a ) = 1 2 6 , or a 2 − 3 6 a + 1 2 6 = 0 . By the quadratic formula, a = 2 3 6 ± 7 9 2 .
Plugging in a = c − 1 2 into c ( 4 8 − a ) = 7 0 2 gives c ( 6 0 − c ) = 7 0 2 , or c 2 − 6 0 c + 7 0 2 = 0 . By the quadratic formula, c = 2 6 0 ± 7 9 2 .
Now consider these ± 's. It is easy to verify that both must be negative because a + c < 4 8 . Therefore, a = 2 3 6 − 7 9 2 and c = 2 6 0 − 7 9 2 . Then b = 4 8 − a − b = 7 9 2 , so the desired answer is H I 2 = b 2 = 7 9 2 .
Note A B = A D + D E + E B = 3 + 3 9 + 6 = 4 8 , which is the side length of equilateral △ A B C . By the secant theorem, B F ⋅ B G = B E ⋅ B D = 6 ( 6 + 3 9 ) , so B F ( B F + 2 1 ) − 2 7 0 = ( B F + 3 0 ) ( B F − 9 ) = 0 . Hence B F = 9 and C G = B C − B F − F G = 4 8 − 9 − 2 1 = 1 8 . We apply the secant theorem again to obtain the system C H ( C H + H I ) A I ( A I + H I ) C H + H I + I A = C G ⋅ C F = 1 8 ( 3 9 ) , = A D ⋅ A E = 3 ( 4 2 ) , = 4 8 . This gives C H ( 4 8 − I A ) = 1 8 ( 3 9 ) and I A ( 4 8 − C H ) = 3 ( 4 2 ) , and subtracting the latter from the former yields C H − I A = 1 2 . Hence 4 8 = ( I A + 1 2 ) + H I + I A , or I A = 1 8 − 2 H I . Finally, we obtain 3 ( 4 2 ) = I A ( H I + I A ) = ( 1 8 − 2 H I ) ( 1 8 + 2 H I ) = 1 8 2 − 4 H I 2 , or ∣ H I ∣ 2 = 4 ⋅ 3 2 ( 6 2 − 1 4 ) = 7 9 2 .
Notice that the computations are simplified with this approach, even though the basic method remains the same. We could have simplified the computation even further by recognizing all given lengths were multiples of 3, so we could have scaled the diagram by that factor and reintroduced it at the end.
We're going to use something called the Intersecting Secants Theorem (also known as the secant-secant theorem) which tells us that when two secant lines intersect each other outside a circle, the products of their segments are equal.
Now notice that D B and G B are two secants of the circle Γ and they intersect at a point outside Γ , B .
So the intersecting secants theorem tells us:
B D ⋅ B E = B G ⋅ B F
⇒ ( B E + B D ) ⋅ B E = ( B F + F G ) ⋅ B F
Plugging in all the values gives us:
B F 2 + 2 1 B F − 2 7 0 = 0 .
Solving this we get B F = 9 .
Again notice that the sides of the equilateral triangle are equal to 4 8 [because A B = A D + D E + E B = 3 + 3 9 + 6 = 4 8 ].
So, C G = 4 8 − F G − B C = 4 8 − 2 1 − 9 = 1 8 .
Again, F C and I C are two secants of the circle Γ and they intersect at C .
So, C F ⋅ C G = C I ⋅ C H
⇒ ( 2 1 + 1 8 ) ⋅ 1 8 = C I ⋅ C H
⇒ 7 0 2 = C I ⋅ C H ⋯ ( 1 ) .
We have another set of secants. Take E A and H A .
So, A E ⋅ A D = A H ⋅ A I
⇒ ( 3 + 3 9 ) ⋅ 3 = ( 4 8 − C H ) ( 4 8 − C I )
⇒ 1 2 6 = 4 8 2 − 4 8 ( C I + C H ) + C I ⋅ C H
From ( 1 ) , C I ⋅ C H = 7 0 2 .
So making this substitution, we get:
1 2 6 = 2 3 0 4 − 4 8 ( C I + C H ) + 7 0 2
⇒ ( C I + C H ) = 4 8 2 3 0 4 + 7 0 2 − 1 2 9 = 6 0 .
Squaring both sides gives us:
( C I + C H ) 2 = 6 0 2 = 3 6 0 0
⇒ ( C I − C H ) 2 + 4 ⋅ C I ⋅ C H = 3 6 0 0 .
Again recall ( 1 ) which allows us to substitute C I ⋅ C H with 7 0 2 . Also notice that C I − C H = H I . So we're almost done!
Plugging in all the values gives us:
H I 2 = 3 6 0 0 − 4 ⋅ 7 0 2 = 7 9 2 .
I solved using Pythagoras' Theorem on the 6 triangles AOB, BOC, COD, DOE, FOG and HOI; and using the fact that OD=OE=OF=OG=OH=OI, where O is the centre. It is a fair bit more working than the secant idea though, glad I didn't take the hour to type it out :)
using coordinate geometry can also help to solve this problem
Log in to reply
Yes. A lot of problems can be approached in multiple ways. Personally, I feel more at home with elementary Euclidean geometry.
I also did the same as Mursalin H did
I would like to know if there is another method
I used Co ordinate geometry , though it becomes lengthy and please forgive me I cant type a big solution. Mursalin's method is simpler than mine. Actually I first tried euclidean geometry only but the idea didn't click, so went for co ordinate geometry approach, it was bit easier as its an equilateral triangle and you can always choose your co ordinate axes such that the abscissa coincides with the base
From power of a point on B , we have B E ⋅ B D = B F ⋅ B G , hence 6 ⋅ 4 5 = B F ( B F + 2 1 ) ⇒ B F = 9 . 4 8 = A B = B C = 9 + 2 1 + G C , so G C = 1 8 . Using power of a point on C , we obtain C G ⋅ C F = C H ⋅ C I ⇒ 1 8 ⋅ 3 9 = C H ( C H + H I ) . Similarly, we have 3 ⋅ 4 2 = A I ( A I + H I ) . Letting C H = a , H I = b and I A = c , we have 1 8 ⋅ 3 9 = a ( a + b ) , 3 ⋅ 4 2 = c ( c + b ) and a + b + c = 4 8 . Because a + b = 4 8 − c and b + c = 4 8 − a , we can substitute to get 7 0 2 = a ( 4 8 − c ) and 1 2 6 = c ( 4 8 − a ) . Subtracting these yields 1 2 = a − c ⇒ a = 1 2 + c . Plugging this back into 1 2 6 = c ( 4 8 − a ) gives us 1 2 6 = c ( 3 6 − c ) ⇒ c = 1 8 − 3 2 2 , therefore a = 3 0 − 3 2 2 . H I 2 = ( 4 8 − ( 1 8 − 3 2 2 ) − ( 3 0 − 3 2 2 ) ) 2 = ( 6 2 2 ) 2 = 7 9 2 .
Let BF=x. By power of a point, (BE)(BD)=(BF)(BG). (6)(45)=x(x+21). After simplification and factorization, x=-30, 9. We discard -30 to find BF=9. The triangle's side length is 48, so 9+21+GC=48. GC=18. Let AI=a, HI=b, and CH=c. a+b+c=48. By power of a point, (3)(42)=a(a+b). Also, (18)(39)=c(b+c). Three variables, three equations: solve for b (and a/c along the way). Substituting 48-c for a+b and 48-a for b+c makes the process easier. After simplification, a=18-sqrt(198), c=30-sqrt(198). Therefore, b=sqrt(798). b^2=798, and we are done.
1st power of point B w.r.t. Circle is BE(BE+ED) OR also BF(BF+FG) . Hence solving this eqn. we get BF=9,as the tri. Is eqlateral GC=18 and
AI+HI+CH=48
let AI=x, HI=y,CH=z
applying eqn. Of power of point w.r.t. A and then C we get 2 eqn.
x^2 +xy-126=0.......1
z^2+zy-702=0..........2
subtracting these 2 eqn. And solving we get
z-x=12 .........3
we have z+x=48-y...........4
eq3 +eq4 we get
z = 30 - y/2
putting these value in eq. 2 we obtain-
y^2 =|HI|^2 =792
We use power of a Point from B E . Since B E ∗ B D = B F ∗ B G , 6 ∗ 4 5 = B F ∗ ( B F + 2 1 ) , so B F = 9 . Since A B C is equilateral, A B = 4 8 , so B C = A C = 4 8 , which means that G C = 1 8 . By power of a point from A, we get that 3 ∗ 4 2 = A I ∗ ( 4 8 − H C ) , and power of a point from C gives 1 8 ∗ 3 9 = C H ∗ ( 4 8 − A I ) , so solving we have that H I = 7 9 2 so our answer is 792.
The secant secant theorem for the chords ED, GF and the outside point B, says that: |EB|⋅|DB|=|GB|⋅|FB|. |GB|=|FB|+|FG| => |EB|⋅|DB|=|FB|⋅(|FB|+|FG|) => |FB|⋅(|FB|+21)=6⋅(6+39)=270 => |FB|=9. ABC is an equilateral triangle => |AB|=|BC|=|CA|=|EB|+|DE|+|AD|=6+39+3=48=|FB|+|FG|+|GC| => |GC|=18. The secant secant theorem for the chords FG, HI and the outside point C: |GC|⋅|FC|=|HC|⋅|IC| =>|HC|⋅(|HC|+|HI|)=18⋅(18+21)=702, but |HC|+|HI|+|IA|=|AC|=48 => |HC|+|HI|=48-|IA|. Hence, |HC|⋅(48-|IA|)=702. (1) Applying the secant secant theorem again - this time for the chords DE, IH and the outside point A - we get that |DA|⋅|EA|=|IA|⋅|HA| => 3⋅(3+39)=|IA|⋅(|IA|+|HI|), but |IA|+|HI|=48-|HC| => |AI|⋅(48-|HC|)=126. (2) Substracting the relations (1) and (2), we obtain that 48⋅(|HC|-|IA|)=702-126=576 => |HC|-|IA|=12. Replacing |HC| with 12+|IA| in the second relation, we get that: |IA|⋅(48-12-|IA|)=126 => |IA|^2-36⋅|IA|+126=0 => |IA|=18-3√22. |HI|=48-|IA|-|HC|=48-|IA|-12-|IA|=36-2⋅|IA|=36-(36-6√22)=6√22. Hence, |HI|^2=36⋅22=792.
Please use L A T E X . This solution is difficult to read
Using Secant Theoram
( 3 9 + 6 ) ⋅ 6 ⇒ B F 2 + 2 1 B F − 2 7 0 And, BF is a length, hence B F = 9 a n d C G Now, y ( x + y ) And, ( 4 8 − y ) × [ 4 8 − ( x + y ) ] Solving.... x And, since the distance is positive, ∣ H I ∣ 2 = 7 9 2 = B F ⋅ ( B F + 2 1 ) = 0 positive = 1 8 = 1 8 × 3 9 = 4 2 × 3 = ± 6 2 2 ∣ H I ∣ = 6 2 2
Moderator note:
Yes, it's just using power of a point many times, to figure out the relationship between the lengths.
Is it possible to determine the radius of this circle? I got a frightening number such as (7/19)(8479/3)^(1/2) or R ~=19.59. Can anyone please confirm this? If it's wrong what would be correct radius?
AB= 48 triangle BDF and BGE are similar. BE : BG = BF: BD and BF \times BG = BE \times BD BF \times (BF+21) = 270
=> BF=9 [ BF= -30 rejected]
CH \times CI = CG \times CF AI \times AH = AD \times AE note :- let CH = x , HI = y , IA = z
x \times (x+y) = 702 - eq 1. z \times (z+y) = 124 - eq 2. x+y+z = 48 - eq 3.
from eq 3. z= 48-x-y
and from eq 1. y = \frac { (702 - x^2)}{x}
putting value of z and y in eq .2
(48-x-y) \times ( 48-x-y+y) = 124 also, putting value of y in upper eq. we get,
(48 - x - \frac { (702 - x^2)}{x} ) \times (48 - x ) = 124
on solving for x , we putting the value in y = \frac { (702- x^2)}{x} we get, y^2 = \frac { 459073}{576} => y = 791.57 .
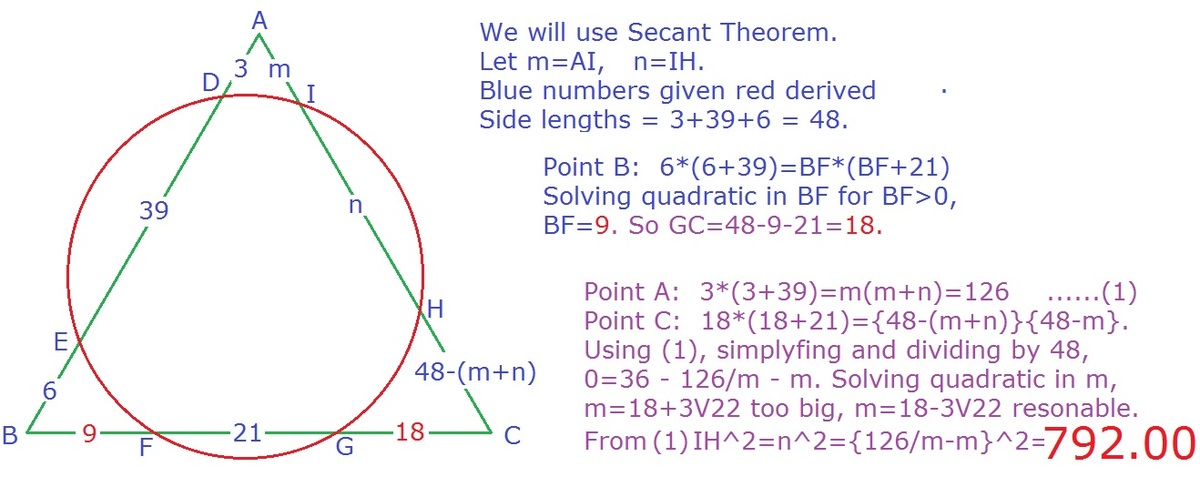
The side length of the equilateral triangle is 3+39+6=48. The power of A with respect to Γ is A D ⋅ A E = 3 ( 3 + 3 9 ) = 1 3 6 . The power of B with respect to Γ is B D ⋅ B E = ( 3 9 + 6 ) 6 = 2 7 0 . Let B F = x , then by the power of a point theorem, B F ⋅ B G = 2 7 0 , so x ( x + 2 1 ) = 2 7 0 . The only positive solution is x = 9 . Since the side length is 48, C G = 4 8 − 2 1 − 9 = 1 8 . Therefore, the power of C with respect to Γ is C G ⋅ C F = 1 8 ( 1 8 + 2 1 ) = 7 0 2 .
Let A I = a , C H = b , then by power of a point theorem a ( 4 8 − b ) = 1 3 6 b ( 4 8 − a ) = 7 0 2 Subtract those two equations and divide by 48 to get b − a = 1 2 . Substitute this into the first equation to get a quadratic in a . The quadratic equation has solutions a = 1 8 ± 3 2 2 , so b = 3 0 ± 3 2 2 . Since a + b < 4 8 , the solution with the negative sign is taken, giving H I = 4 8 − a − b = 6 2 2 . Therefore ∣ H I ∣ 2 = 7 9 2 .