Circle fun
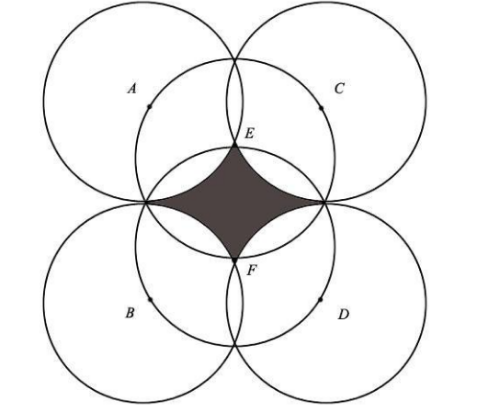
If all circles with centers A , B , C , D , E and F have the same radius of 7, what is the area of the shaded region given that circles E and F pass through the centers of the other circles and that ABCD forms a rectangle (when joining up those points with lines).
Give answers to at least one decimal place.
The answer is 24.680374339.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Sidenote: The 60 degrees also arises from the formation of equilateral triangles which arise from the fact that the circles have equal radii.
"All angles are 60 degrees, as the following lines cut the circle into 6 equal parts, hence the angle is 360/6 = 60 deg," is bad reasoning. I wrote this a while ago so apologies. I believe that using the fact that circles have equal radii by joining up lines of equal length 7 create the equilateral triangles proving that the angle involved in the circle segment calculation is 60 degrees.
In my opinion the problem was explained ambiguously. It is not enough to say that circles E and F pass through the centres of the other circles. The idea is complete if you add two additional circles (e.g.
G
,
H
) with the same assumptions (the circles pass through the centers of the other circles). See the figure below.
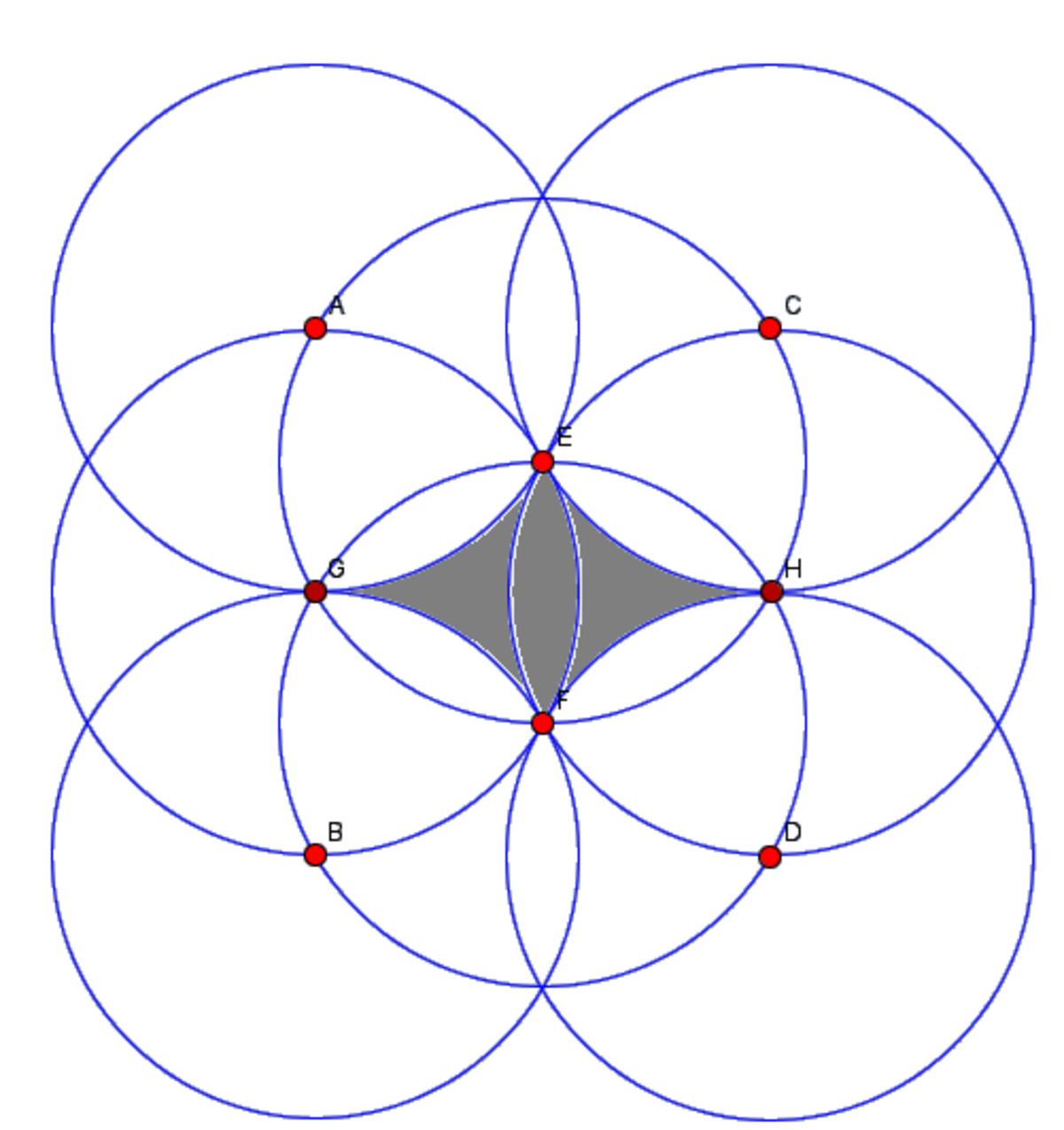 The answer is:
The answer is:
2 4 3 r 2 − 4 1 2 r 2 ( 2 π − 3 3 ) = 2 4 . 6 8 0 3 7 4 3 3 9
You're right. I've updated the description to say that ABCD forms a rectangle.
I think you should at least point out that circles E and F passes through the centers of the other 4 circles. I missed that detail the first time I tackled this. Once I saw that missed detail, the rest more or less followed.
oops! Thanks, ill update it now.
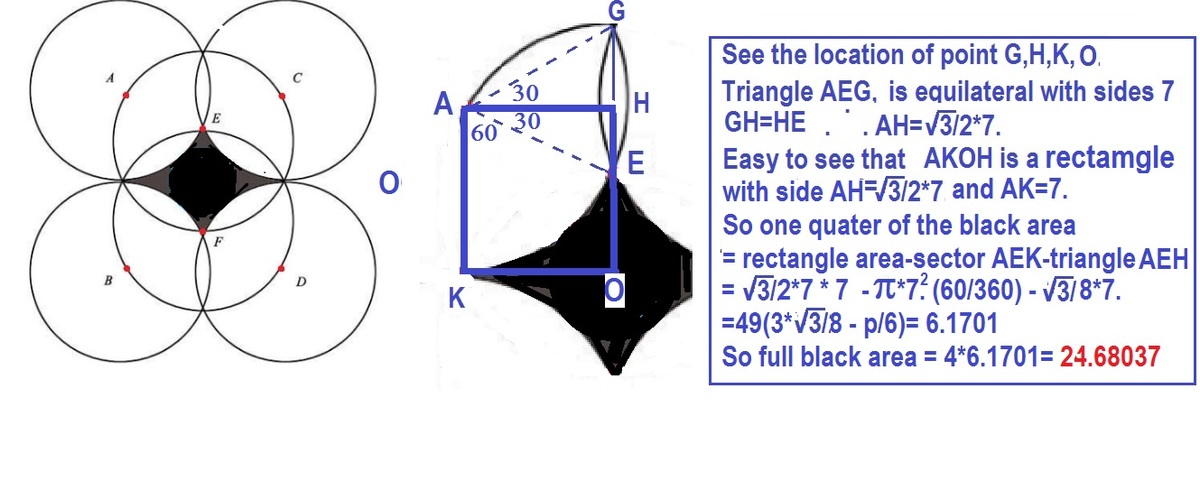
All angles are 60 degrees, as the following lines cut the circle into 6 equal parts, hence the angle is 360/6 = 60 deg,
Therefore,
Area of Shaded Region = The two triangles - Half of the four "lips"
Area of one "half lip":
The shape of a segment arises, and so, using the formula for area of a segment...
Angle = 60 deg = 3 π radians
Therefore,
Half the area of one lip = ( 2 7 2 )*( ( 3 π ) - sin( 3 π ) )
Area of one triangle(Using pythagorean theorem) = ( 2 1 x 7 x sqrt{ 7 2 − 3 . 5 2 } )
So, Area of shaded region = (2 x triangle areas) - (4 x "half lip" areas) = 24.68037...