Circle Geometry Question
In the figure below, there is a semicircle with radius 2 and two identical semicircles within it, each with radius 1. The smaller semicircles are externally tangent to each other and share the edge with the larger semicircle. There is also a circle tangent to all three semicircles (internally tangent to the large semicircle, and externally tangent to the smaller semicircles).
What is the radius of the circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
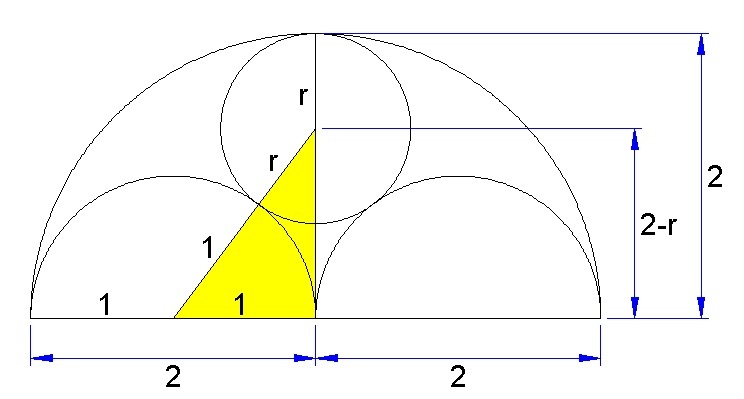 Applying
pythagorean theorem
on the right triangle formed (color yellow), we have
Applying
pythagorean theorem
on the right triangle formed (color yellow), we have
( 1 + r ) 2 = 1 2 + ( 2 − r ) 2
1 + 2 r + r 2 = 1 2 + ( 4 − 4 r + r 2 )
1 + 2 r + r 2 = 1 + 4 − 4 r + r 2
2 r + 4 r = 4
6 r = 4
r = 6 4 = 3 2
nice solution...
Product of exterior part of secant with its entire length is equal to the square of tangent. So, r(2+r) = (2 - r)^2, => 2r = 4 - 4r, or r = 2/3.
We have formed a 90 degree triangle with hypotenuse (r+1) and sides 1 and 2-r (radius of large circle - radius of small circle).
We can form a Pythagorean Equation:
(r+1)² = 1 + (2-r)²
r² + 2r + 1 = 1 + 4 - 4r + r²
Cancel out the one and the r²
2r = 4 - 4r
6r = 4
r = 3 2