Circle gets cozy in triangle
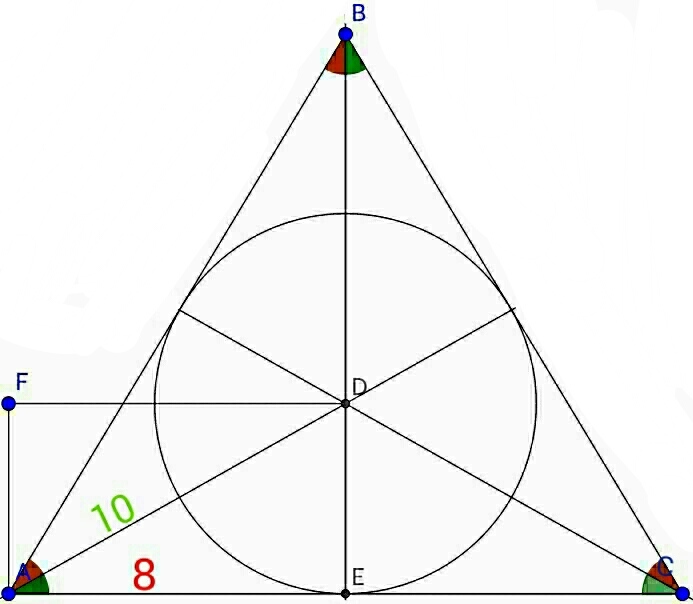
In
,
,
and
are the bisectors of
,
and
respectively.
If
is a rectangle such that
and
, find the area of the circle inscribed in
.
Round your answer( in ) to the nearest integer.
The answer is 113.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We know that incenter is the point of intersection of the angular bisectors. So, D is the incenter of △ ABC Now, since AFDE is a rectangle, ∠ AEB = 9 0 ∘ . So, DE is the inradius.
Using pythagoras' theorem:-
AD 2 DE DE DE = AE 2 + DE 2 = 1 0 2 − 8 2 = 3 6 = 6
So, area of incircle = π r 2 = 7 2 2 × 6 2 = 1 1 3 . 1 4 2 ≈ 1 1 3 cm 2