Circle in a quarter circle
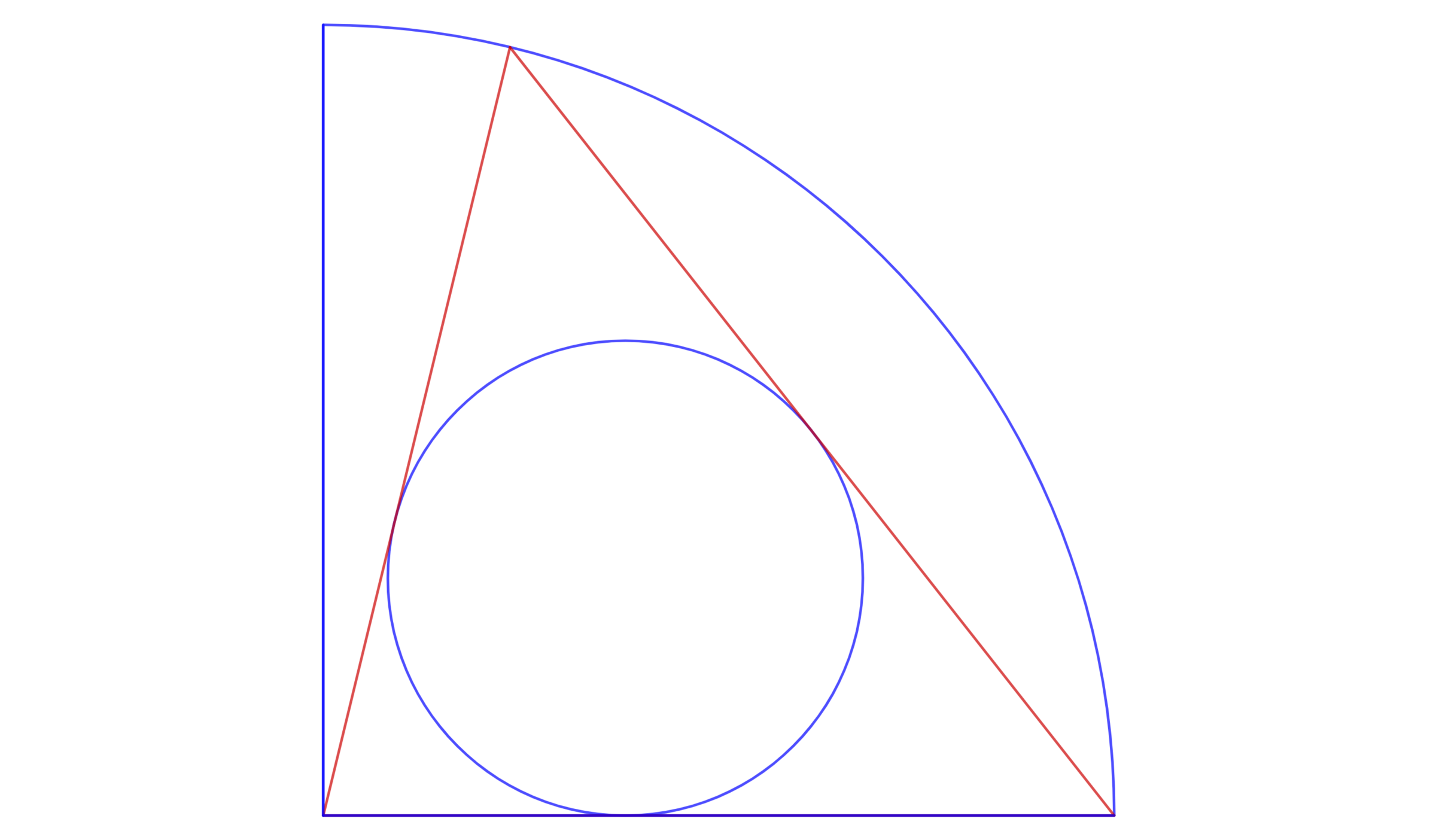
A triangle is inscribed in a quarter circle of radius 1, as shown in the figure. What is the radius of the largest circle which can be inscribed in such a triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
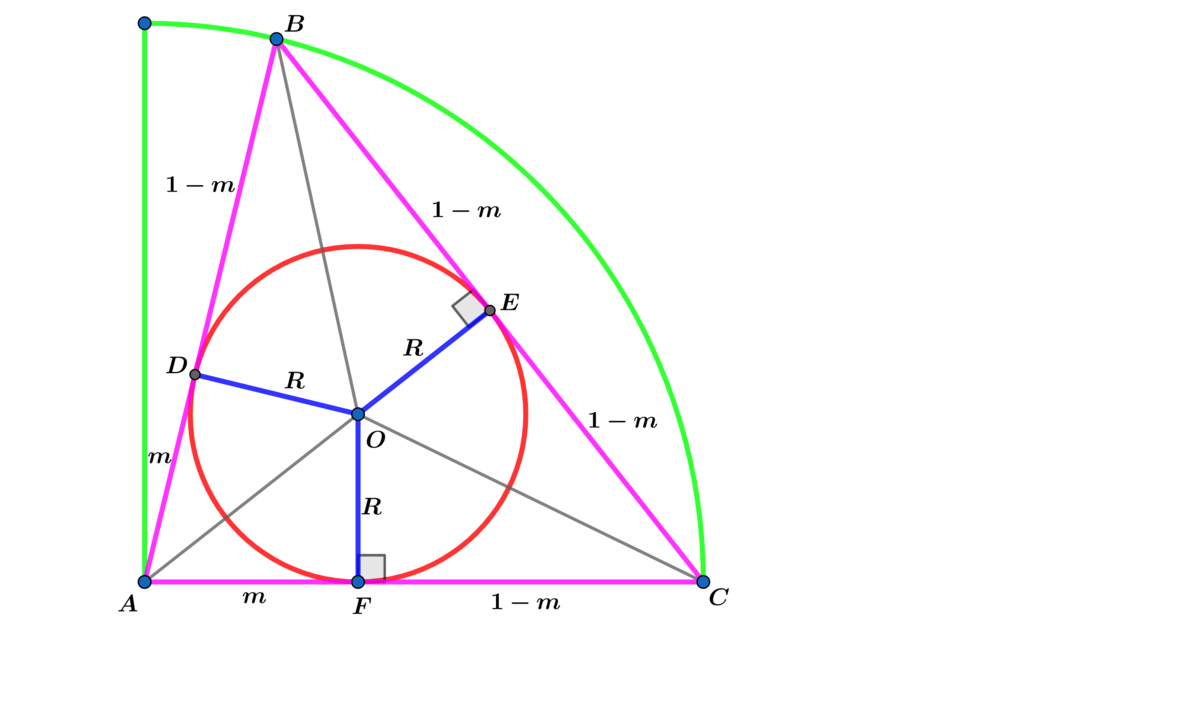
Using the radii of the inscribed circle ⟹ A △ A B C = ( 2 − m ) R and using Heron's Formula
⟹ A △ A B C = ( 2 − m ) ( 1 − m 2 ) m
⟹ R = 2 − m ( 1 − m ) m ⟹ d m d R = 2 m 2 1 ( 2 − m ) 2 3 2 ( m 2 − 3 m + 1 ) = 0 ⟹ m = 2 3 ± 5
and 0 < m < 1 ⟹ m = 2 3 − 5 ⟹ R m a x = ( 2 5 − 1 ) 2 5
Note: You can check that a max does occur at m = 2 3 − 5 .
I posted my solution as a comment since Brilliant is not working properly in the last couple of days. Having a problem posting my solutions.
Does anyone know when we be able to download our problems and solutions? The download option should have been posted today(6/11/21).
Is it possible that Chew-Seong Cheong can create a wordpress blog shared by brilliant?
A triangle 'petal' of a square is the one with the largest possible area that can be inscribed in a larger quarter circle, but its incircle can't be the biggest because the petal itself is not optimising the convex area available in the quarter (see why traditionalists are called squares, they're mostly thinking in one direction of two dimensions for the petal area but not the incircle itself). A triangle 'petal' of a hexagon on the other hand is "too optimised" that we can fill in another circle the size of its incircle if we have the full 6 petals in all 4 quarters (in the middle of all 6 incircles), such that we can safely assume that this arrangement is more communal / social-centric and less individual. With a pentagonal petal as the middle ground, seeing the √5 is golden enough to choose the above option of ((√5 – 1)/2)^(5/2).
thinking outside the (square) box!
Since two sides of the triangle are the same as the quarter circle's radius of 1 , it is an isosceles triangle.
If the triangle's vertex angle is θ , then its base is 2 sin 2 1 θ , so that its perimeter is P = 2 + 2 sin 2 1 θ and its area is A = 2 1 ⋅ 1 2 ⋅ sin θ = sin 2 1 θ cos 2 1 θ .
That means its inradius is r = P 2 A = 2 + 2 sin 2 1 θ 2 sin 2 1 θ cos 2 1 θ = 1 + sin 2 1 θ sin 2 1 θ cos 2 1 θ .
Letting x = sin 2 1 θ , cos 2 1 θ = 1 − sin 2 2 1 θ = 1 − x 2 and r = 1 + x x 1 − x 2 .
The largest radius r will occur when r ′ = − ( x + 1 ) 1 − x 2 x 2 + x − 1 = 0 , which solves to x = 2 5 − 1 = ϕ − 1 = ϕ 1 for x > 0 .
This makes the largest radius r = 1 + x x 1 − x 2 = 1 + x x 2 ( 1 − x ) = ϕ ϕ 2 1 ⋅ ϕ 2 1 = ϕ 5 1 = ( 2 5 − 1 ) 5 / 2 .
Let the triangle inscribed in the unit quarter circle be A B C , ∠ A = θ , and the radius of the incircle be r . Then
r d θ d r 2 cos θ ( 1 + sin 2 θ ) 2 ( 1 − 2 sin 2 2 θ ) ( 1 + sin 2 θ ) 1 − 2 sin 2 2 θ sin 2 2 θ + sin 2 θ − 1 ⟹ sin 2 θ cos 2 θ = s A = 2 1 ( 1 + 1 + 2 sin 2 θ ) 2 1 ⋅ 1 2 ⋅ sin θ = 2 + 2 sin 2 θ sin θ = ( 2 + 2 sin 2 θ ) 2 cos θ ( 2 + 2 sin 2 θ ) − sin θ cos 2 θ = sin θ cos 2 θ = 2 sin 2 θ ( 1 − sin 2 2 θ ) = sin 2 θ ( 1 − sin 2 θ ) = 0 = 2 5 − 1 = φ − 1 = φ 1 = 1 − φ 2 1 = 1 − φ φ − 1 = φ 1 where A and s are the area and semiperimeter of △ A B C . To find max ( r ) Putting d θ d r = 0 where φ denotes the golden ratio.
Therefore
max ( r ) = 2 + 2 sin 2 θ sin θ = 2 + 2 ( φ − 1 ) φ φ 2 = ( φ 1 ) 5 / 2 = ( 2 5 − 1 ) 5 / 2