Circle in a rectangle

We drop perpendiculars from $O$ the diagonal. Then $\angle AFE=\angle OFG$ and $\angle AEF=\angle FGO=90°$ . Since $OG$ is a radius of the circle, and $AE=OX=OG$ , the $AEF$ and $FGO$ triangles are coincident. Similarly the $OGH$ , $IHC$ triangles are coincident too. So $[OIDE]=[ACD]=\dfrac{1}{2}[ABCD]$ .

So the two area is equal.

If we set the base of the rectangle to be $a$ and the height as $1$ , from Heron's formula, the radius of the circle will be $R=\dfrac a{1+a+\sqrt{1+a^2}}$

The area of the rectangle will be $\color{#3D99F6} A_{\square}$ $=(1-R)(a-R)$

And the yellow area will become $\color{#CEBB00} A_{hex}$ $=aR+R-R^2$

Their difference $A=\color{#3D99F6} A_{\square}$ $-\color{#CEBB00} A_{hex}$ $=a-2aR-2R+2R^2$

$A=\dfrac 1{(1+a+\sqrt{1+a^2})^2}\left(a(1+a+\sqrt{1+a^2})^2-2a^2(1+a+\sqrt{1+a^2})-2a(1+a+\sqrt{1+a^2})+2a^2\right)=0$

Consider a $3 \times 4$ rectangle.

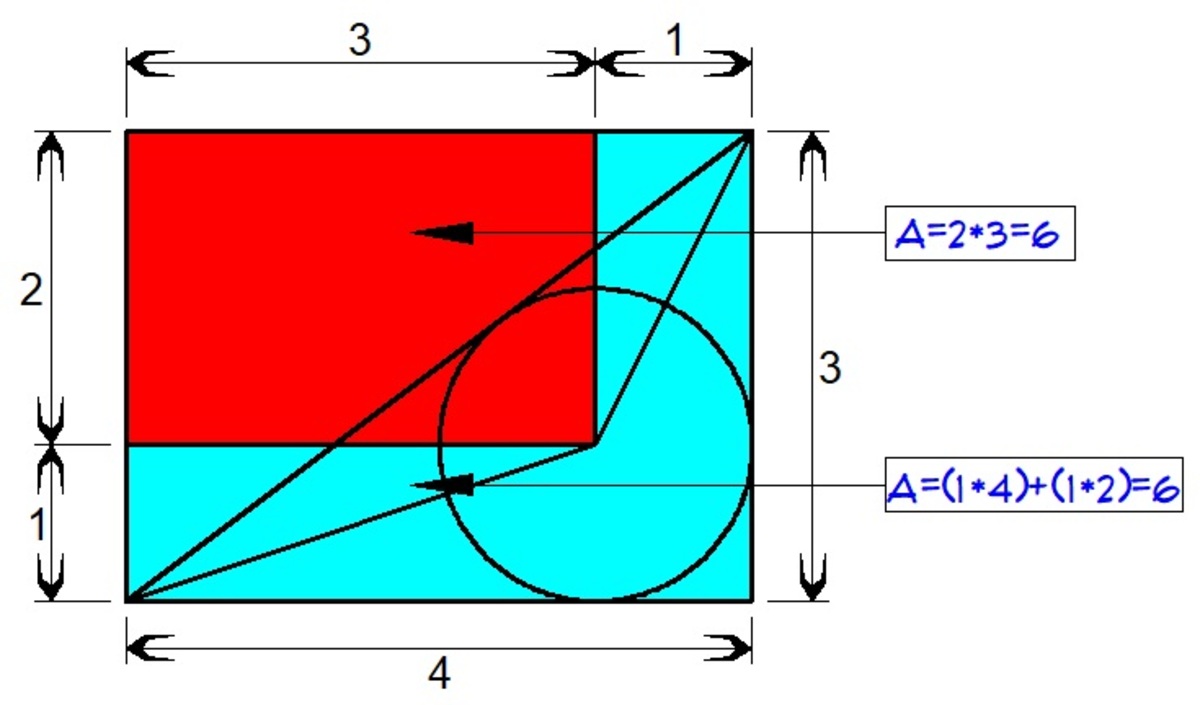
Measuring diagonal length by two methods and equating them also provides the solution.
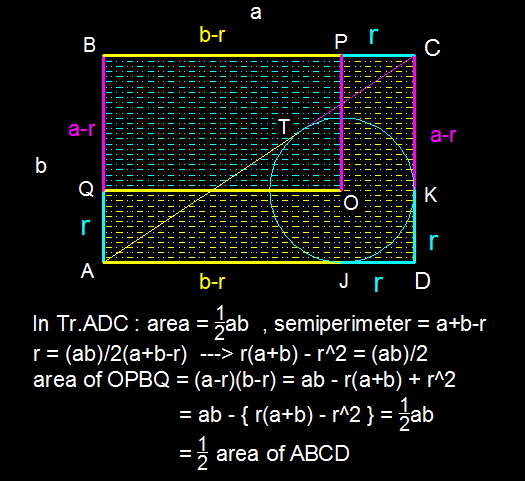
Diagonal length = sum of lengths of two tangents = (a-r) + (b-r), where a and b are side lengths of rectangle and r is radius.
Diagonal length is also √(a^2+b^2).
Squaring and equating the two gives,.
(a-r)^2 + (b-r)^2 + 2(a-r)(b-r) = a^2 + b^2.
2(a-r)(b-r) = {a^2-(a-r)^2} + {b^2-(b-r)^2}.
= r(2a-r) + r(2b-r) = 2r(a+b-r).
Or, (a - r)(b - r) = r(a + b - r).
But LHS is equal to Blue area and RHS is equal to Yellow area.
So, Blue area = Yellow area