Circle in Quarter Ellipse
Take the ellipse
1 4 4 x 2 + 4 9 y 2 = 1
in the first quadrant, and inscribe a circle in it, such that the circle is tangent to the x -axis , y -axis, and the ellipse. This is shown in the figure below.
Find the radius of the circle. If the radius is r , input ⌊ 1 0 5 r ⌋
You may need to resort to numerical methods.
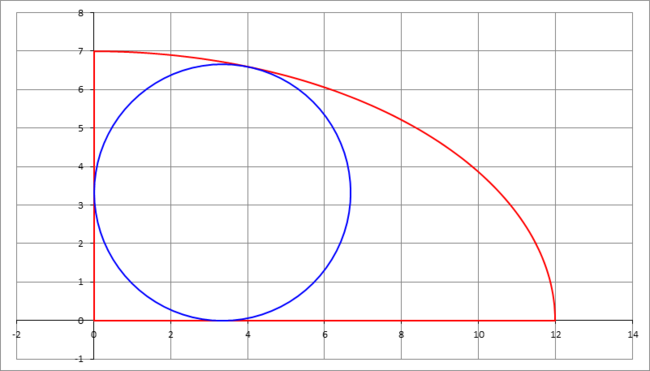
The answer is 333348.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The point of intersection of the circle and ellipse satisfies three equations: 1 4 4 x 2 + 4 9 y 2 ( x − r ) 2 + ( y − r ) 2 − 1 4 4 y 4 9 x = 1 = r 2 = − y − r x − r where the last equation comes from setting the slopes of the tangent lines to the circle and ellipse equal to each other.
This becomes three quadratic equations in three unknowns, which any computer algebra system can easily solve. I used MAGMA's GroebnerBasis to get an equation for r , namely r 8 − 5 7 9 r 6 + 3 4 1 3 1 r 4 − 1 7 4 1 8 2 5 r 2 + 1 5 9 2 0 1 0 0 = 0 , which has four real roots, ± 3 . 3 3 3 4 8 … and ± 2 2 . 7 9 5 9 8 … . The former is clearly the radius of the inscribed circle, and the latter is the radius of the circle outside the ellipse centered at ( r , r ) of radius r that is tangent to the ellipse at one point. So the answer is 3 3 3 3 4 8 .
Since it's tangent to the axes, the equation of the circle is ( x − r ) 2 + ( y − r ) 2 = r 2
From the equation for an ellipse with semi-axes a , b , y = b 1 − a 2 x 2
Substituting this into the equation for the circle (and expanding) we get x 2 − 2 r x + b 2 ( 1 − a 2 x 2 ) − 2 b r 1 − a 2 x 2 + r 2 = 0
We want this to have exactly one real root (corresponding to the point of tangency). This will in fact be a double root (why?), so the easiest thing to do is use a discriminant. Before we can do that, we need to clear square roots above; after some word-processing we get ( a 2 − b 2 ) 2 x 4 − 4 a 2 r ( a 2 − b 2 ) x 3 + 2 a 2 ( a 2 b 2 + 3 a 2 r 2 − b 4 + b 2 r 2 ) x 2 − 4 a 4 r ( b 2 + r 2 ) x + a 4 ( b 2 − r 2 ) 2 = 0
In this case, we get 9 0 2 5 x 4 − 5 4 7 2 0 r x 3 + ( 1 3 4 0 6 4 0 + 1 3 8 5 2 8 r 2 ) x 2 − ( 4 0 6 4 2 5 6 r + 8 2 9 4 4 r 3 ) x + 4 9 7 8 7 1 3 6 − 2 0 3 2 1 2 8 r 2 + 2 0 7 3 6 r 4 = 0
This quartic in x has a multiple root if and only if the discriminant is zero. The discriminant (thanks, Wolfram|Alpha!) is a multiple of 1 5 9 2 0 1 0 0 r 4 − 1 7 4 1 8 2 5 r 6 + 3 4 1 3 1 r 8 − 5 7 9 r 1 0 + r 1 2
Now, r can't be zero, so we can divide through by r 4 to get 1 5 9 2 0 1 0 0 − 1 7 4 1 8 2 5 r 2 + 3 4 1 3 1 r 4 − 5 7 9 r 6 + r 8 = 0
This is a quartic in r 2 so is technically solvable analytically; but checking the positive roots numerically we find the only possible radius is r = 3 . 3 3 3 4 8 3 7 3 … giving the answer 3 3 3 3 4 8 .
(Incidentally, Alpha can give an exact form for this root - but it isn't pretty!)