Circle in Rectangle, what is unshaded Area!!
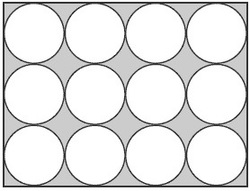 Find the ratio of shaded area to unshaded area in this rectangle containing circles....
Find the ratio of shaded area to unshaded area in this rectangle containing circles....
The answer is 0.27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Another answer would be: let r be the radius of the circle. Since there are 12 circles, so the unshaded area is 12.pir^2. The area of the big rectangle is 8r.6r = 48.r^2. Then, the area of the shaded area is 48.r^2 - 12.pi.r^2 = 12.r^2(4 - pi). Now, the ratio is 12.r^2(4 - pi) / 12.pir^2 = 4-pi / pi This is equal to 0.273239....
It was a really good problem, unfortunately I don't have time so I only used estimation and end up in a wrong but near (maybe) answer - 0.29.
You can actually simplify the answer to (4-pi)/pi which is approximately equal to 0.27 considering a circle with radius r inscribed in a square with side 2r.
No I don't think so, the question is complete.
but the question is not complete
so, let us assume that the radius of each circle is 1. thus, each circle has an area of 3.14 square units. now, let us find the area of the rectangle which has sides of 6 units long and 8 units wide giving us an area of 48 square units. therefore the area of the shaded region is 10.32. now, 10.32/37.68 = 0.27...
Its just 3/11 Assuming π=22/7
Let 'r' be the radius of one circle.
Then:-
Sides of the rectangle are 8r and 6r and its area is 48r^2.
Area of unshaded area is 12 pi r^2.
Area of shaded area is 48r^2-12 pi r^2.
Ratio of shaded area to unshaded area is (48r^2-12 pi r^2)/ (12 pi r^2)
Solving this, you get 0.273
Let r be the radius of one of the circles.
A c i r c l e = π ⋅ r 2
The area of the surrounding square is
A s q u a r e = ( 2 r ) 2 = 4 r 2
The shaded area is the difference between the area of the square and the area of the circle.
A s h a d e d = 4 r 2 − π ⋅ r 2 = ( 4 − π ) r 2
The relation between the shaded area and the unshaded area is
A c i r c l e A s h a d e d = π ⋅ r 2 ( 4 − π ) r 2 = π 4 − π
Which is, approximately, equal to
0.2732395447351626861510701069801148962756771659236515
Out of 12 unshaded circles,let us take only one and consider thjs ciscle( unshased is inscribed in the square).So subtracting area of circle from area of square( consider 2cm one side and radius of circle one cm),we get area of shaded portion as 0.86.for ratio we divide 0.86/3.14 ( with radius 1 area of circle will be 3.14X1 square)that is 0.27.Since there are 12 such circles but ratio of shaded to unshaded will remain the same that is 0.27 Ans K.K.GARG,India
Let the Radius of a circle be 1(unit).
The area of a circle hence becomes pi.
According to what I consider the sides of the rectangle becomes 6 and 8 respectively. The area of unshaded region comes out to be 12pi=37.69911184.Hence the area of unshaded region =Area of Rectangle - Area of the unshaded region
=48-37.69911184=10.30088816.
Now the ratio=10.30088816/37.69911184=0.273239544
4-pi:pi is the answer as a ratio. Answer box will not offer a method of actually entering this answer and question should therefore have been written in such a way that correct answer could be formatted and entered successfully
Lets zoom in on one circle and its surrounding square to calculate the ratio.
Let the diameter of the circle be d
Area of circle π ( 2 1 d ) 2 = 4 π d 2 ≈ 0 . 7 8 5 d 2
As you can see, the circle (unshaded) is approximately 0.785 of the square. Hence, the shaded area is 1 − 0 . 7 8 5 = 0 . 2 1 5 of the square.
The ratio is hence 0 . 7 8 5 0 . 2 1 5 ≈ 0 . 2 7 4