Circle Inscribed in Bell Curves 2
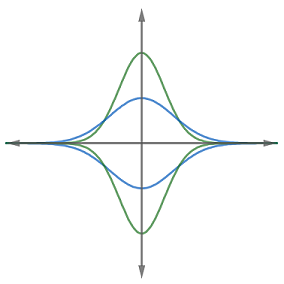
Determine the value of positive real number a so that the area of the circle that is centered at the origin ( 0 , 0 ) and inscribed between the bell curves with equations: y y = a e − a x 2 = − a e − a x 2 is maximized.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Almost perfect solution. Actually, the formula A = 2 a π ( ln 2 a 3 + 1 ) is valid only when a ≥ 1 / 3 2 since x 2 = 2 a ln 2 a 3 ≥ 0 . The complete formula for A is given by A = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ π a 2 , 2 a π ( ln 2 a 3 + 1 ) , 0 < a < 3 2 1 a ≥ 3 2 1
Let r be the distance between a point on the bell curve and the origin. Then by Pythagorean's Theorem, r 2 = x 2 + y 2 . Using implicit differentiation, 2 r d t d r = 2 x + 2 y d x d y which means d x d r = r x + y d x d y .
A circle inscribed by the bell curve would have a minimum radius, so d x d r = 0 , and as the bell curves are symmetrical we only need to examine the first quadrant when y = a e − a x 2 (and therefore when d x d y = − 2 a 2 x e − a x 2 ), so 0 = r x + a e − a x 2 ⋅ − 2 a 2 x e − a x 2 , which solves to x 2 = 2 a ln 2 a 3 for a ≥ 3 2 1 . When 0 < a ≤ 3 2 1 , d x d r is always greater than 0 in the first quadrant, and so its minimum radius is when x = 0 , or when y = a e − a x 2 = a e − a 0 2 = a , or when r = x 2 + y 2 = 0 2 + a 2 = a .
When 0 < a ≤ 3 2 1 , r = a , and the area of the circle is A = π r 2 = π a 2 , and since a is always increasing in the first quadrant, the maximum area would be when a is at its biggest value at a = 3 2 1 , and so the maximum area is A = π a 2 = 3 4 π .
When a ≥ 3 2 1 , since A = π r 2 , r 2 = x 2 + y 2 , y = a e − a x 2 , and x 2 = 2 a ln 2 a 3 , A = π ( x 2 + ( a e − a x 2 ) 2 ) = π ( 2 a ln 2 a 3 + ( a e − a ( 2 a ln 2 a 3 ) ) 2 ) which simplifies to A = 2 a π ( ln 2 a 3 + 1 ) . When the area is maximized, d a d A = 0 , and taking the derivative of A gives d a d A = 2 a 2 3 π − 2 a 2 π ( ln 2 a 3 + 1 ) . Solving 0 = 2 a 2 3 π − 2 a 2 π ( ln 2 a 3 + 1 ) gives a = 3 2 e 2 / 3 . This value of a gives an area of A = 2 a π ( ln 2 a 3 + 1 ) = 2 ( 3 2 e 2 / 3 ) π ( ln 2 ( 3 2 e 2 / 3 ) 3 + 1 ) = 2 e 2 / 3 3 π 3 2 .
Since 2 e 2 / 3 3 π 3 2 > 3 4 π , the value of a that gives the maximum area of a circle inscribed in the given bell curve is a = 3 2 e 2 / 3 .