Circle Inscribed in Bell Curves
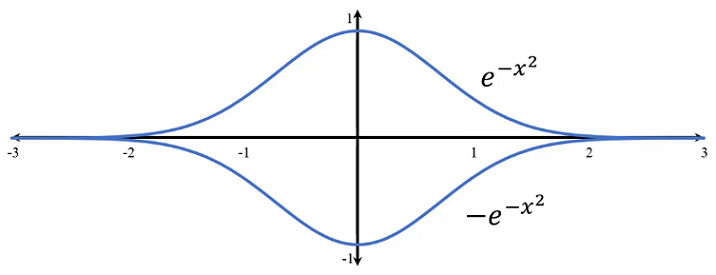
Find the area of the circle that is centered at the origin and inscribed between the bell curves with equations:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the two curves are symmetrical about the origin O ( 0 , 0 ) , let us consider only the first quadrant. Let the distance from O to a point P ( x , y ) on the bell curve be r . Then by Pythagorean theorem, r 2 = x 2 + y 2 . The smallest r is the radius of the circle inscribed within the bell curves. Since r is smallest when r 2 is smallest, we have:
r 2 d x d ( r 2 ) ⟹ 4 x e − 2 x 2 e − 2 x 2 ⟹ x 2 = x 2 + y 2 = x 2 + e − 2 x 2 = 2 x − 4 x e − 2 x 2 = 2 x = 2 1 = 2 ln 2 Differentiate both sides w.r.t. x Equate d x d ( r 2 ) = 0
Note that d x 2 d 2 ( r 2 ) = 2 − 4 e − 2 x 2 + 1 6 x 2 e − 2 x 2 ⟹ d x 2 d 2 ( r 2 ) ∣ ∣ ∣ ∣ x 2 = 2 ln 2 > 0 and r 2 is minimum when x 2 = 2 ln 2 .
The area of the inscribed circle is π r 2 = π ( x 2 + e − 2 x 2 ) = 2 π ( 1 + ln 2 ) .