Circle inscribed in three intersecting lines.
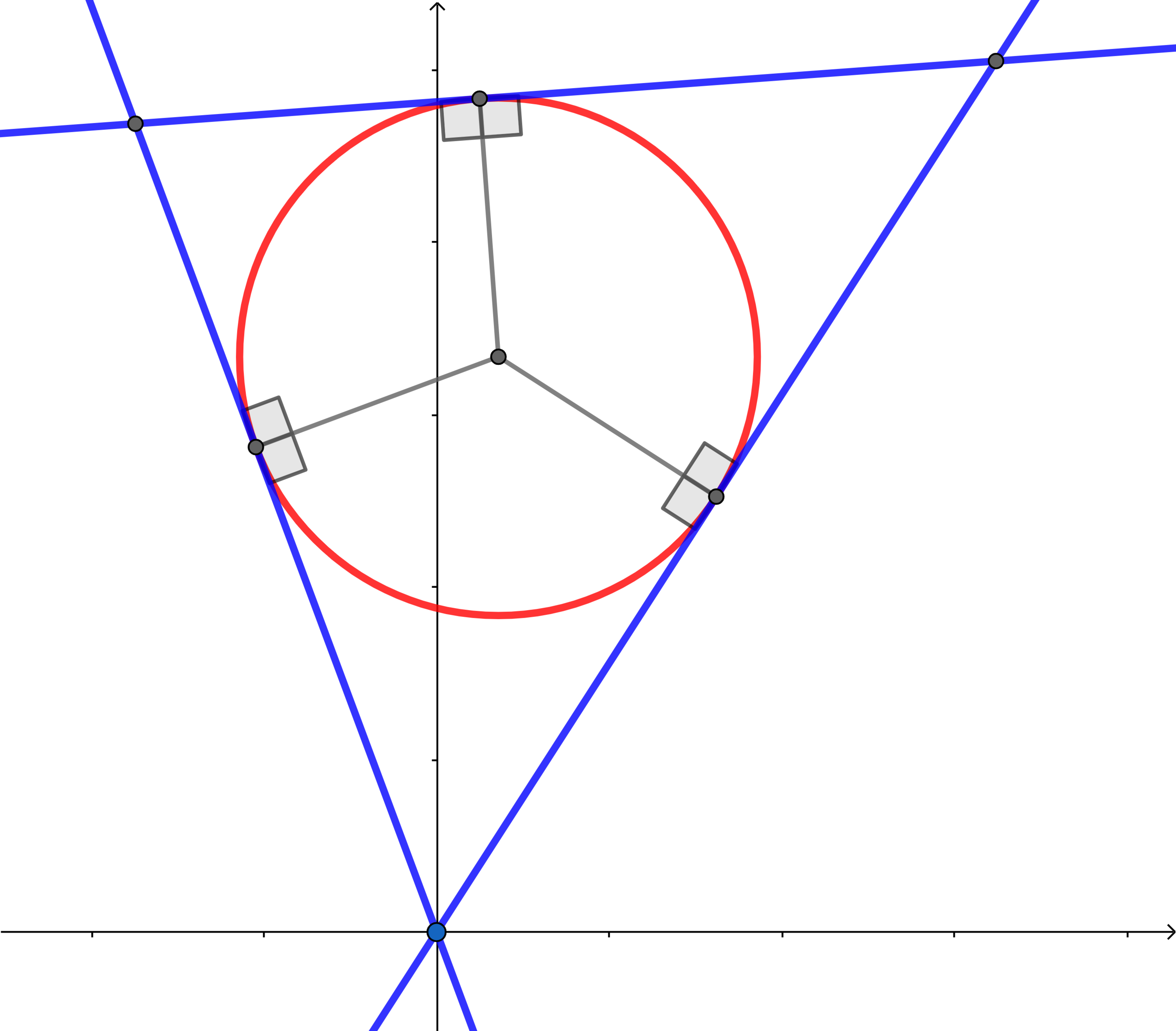
A circle is inscribed in three intersecting lines
( 3 cos ( θ ) − 4 sin ( θ ) ) y − ( 4 cos ( θ ) + 3 sin ( θ ) ) x = 0
( 4 cos ( θ ) − 3 sin ( θ ) ) x + ( 3 cos ( θ ) + 4 sin ( θ ) ) y = 2 4
y cos ( θ ) − x sin ( θ ) = 0 .
If the area of the circle A c = β α π , where α and β are coprime positive integers, find α + β .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
( 1 ) : ( 3 cos ( θ ) − 4 sin ( θ ) ) y − ( 4 cos ( θ ) + 3 sin ( θ ) ) x = 0
( 2 ) : ( 4 cos ( θ ) − 3 sin ( θ ) ) x + ( 3 cos ( θ ) + 4 sin ( θ ) ) y = 2 4
( 3 ) : ( y cos ( θ ) − x sin ( θ ) = 0
This is a fairly basic problem in which I present two methods. The first method I use a rotation thru an angle θ . The second method I just solved the equations in pairs to find the points of intersection.
Method 1:
Using the rotation equations
x = x ′ cos ( θ ) − y ′ sin ( θ )
y = y ′ sin ( θ ) + y ′ cos ( θ )
and replacing the equations above into ( 1 ) , ( 2 ) and ( 3 ) we obtain:
( 1 ′ ) : y ′ = 3 4 x ′
( 2 ′ ) : y ′ = − 3 4 ( x ′ − 6 )
( 3 ′ ) : y ′ = 0
Solving 1 ′ and 2 ′ ⟹ x ′ = y ′ = 0 ⟹ A : ( 0 , 0 )
Solving 2 ′ and 3 ′ ⟹ y ′ = 0 and x ′ = 6 ⟹ C : ( 6 , 0 )
Solving 1 ′ and 2 ′ ⟹ x ′ = 3 and y ′ = 4 ⟹ B : ( 3 , 4 )
⟹ A B = B C = 5 and A C = 6
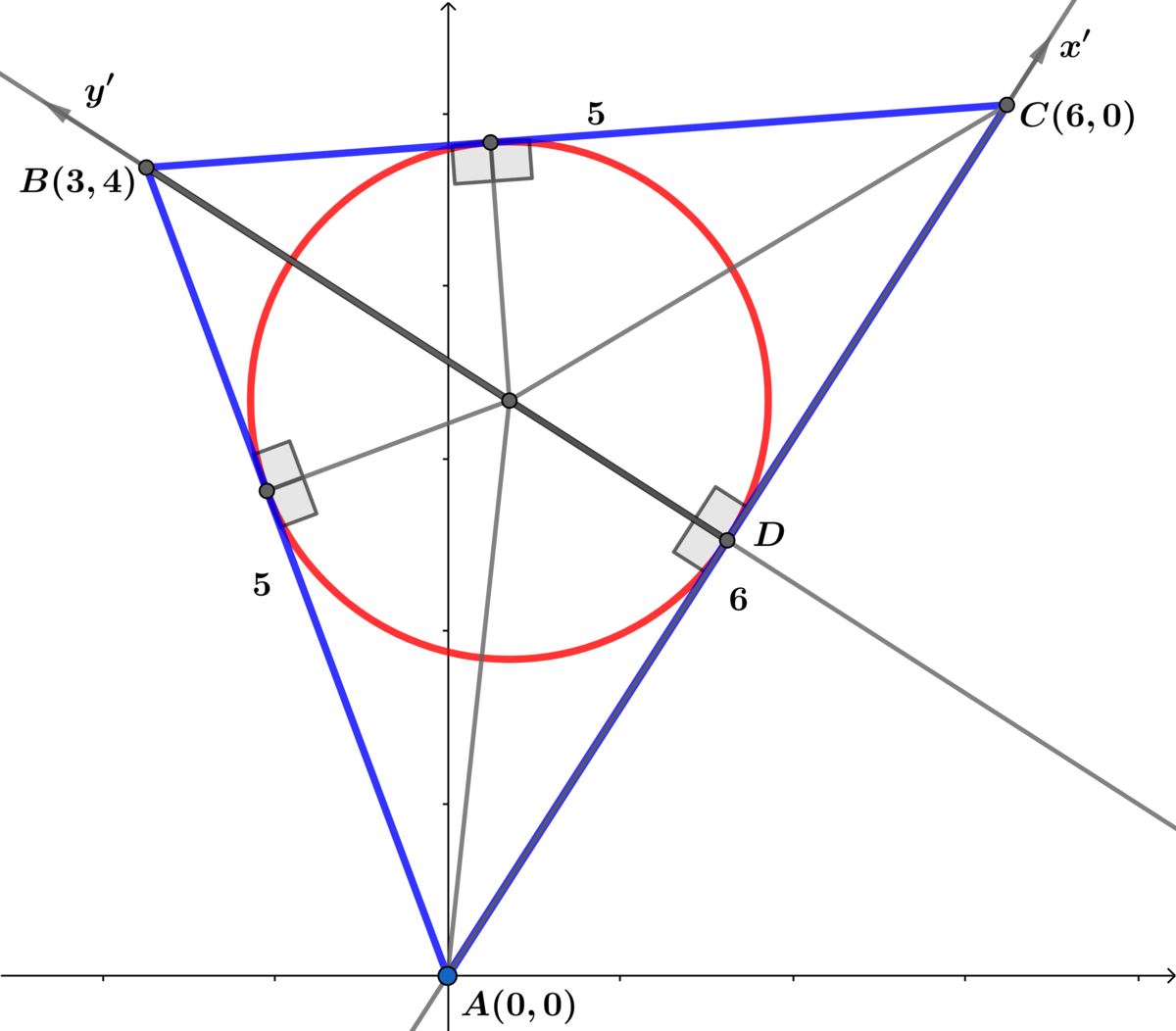
A △ A B C = 2 1 ( 6 ) ( 4 ) = 1 2 = 2 1 r ( 1 6 ) = 8 r ⟹ r = 2 3 ⟹ A c = 4 9 π = β α π
⟹ α + β = 1 3
Method 2:
For ( 1 ) and ( 3 ) :
( 3 ) ⟹ y = x tan ( θ ) ⟹ x = y = 0 ⟹ A : ( 0 , 0 )
For ( 2 ) and ( 3 ) :
( 3 ) ⟹ y = x tan ( θ ) ⟹ x = 6 cos ( θ ) and y = 6 sin ( θ ) ⟹
C : ( 6 cos ( θ ) , 6 sin ( θ ) ) ⟹ A C = 6
For ( 1 ) and ( 2 ) :
− ( 3 cos ( θ ) + 4 sin ( θ ) ) ∗ ( 1 ) + ( 3 cos ( θ ) − 4 sin ( θ ) ) ∗ ( 2 ) ⟹
x = 3 cos ( θ ) − 4 sin ( θ )
and
( 4 cos ( θ ) − 3 sin ( θ ) ) ∗ ( 1 ) + ( 4 cos ( θ ) + 3 sin ( θ ) ) ∗ ( 2 ) ⟹ y = 4 cos ( θ ) + 3 sin ( θ )
⟹ B : ( 3 cos ( θ ) − 4 sin ( θ ) , 4 cos ( θ ) + 3 sin ( θ ) ) ⟹
A B = B C = 5
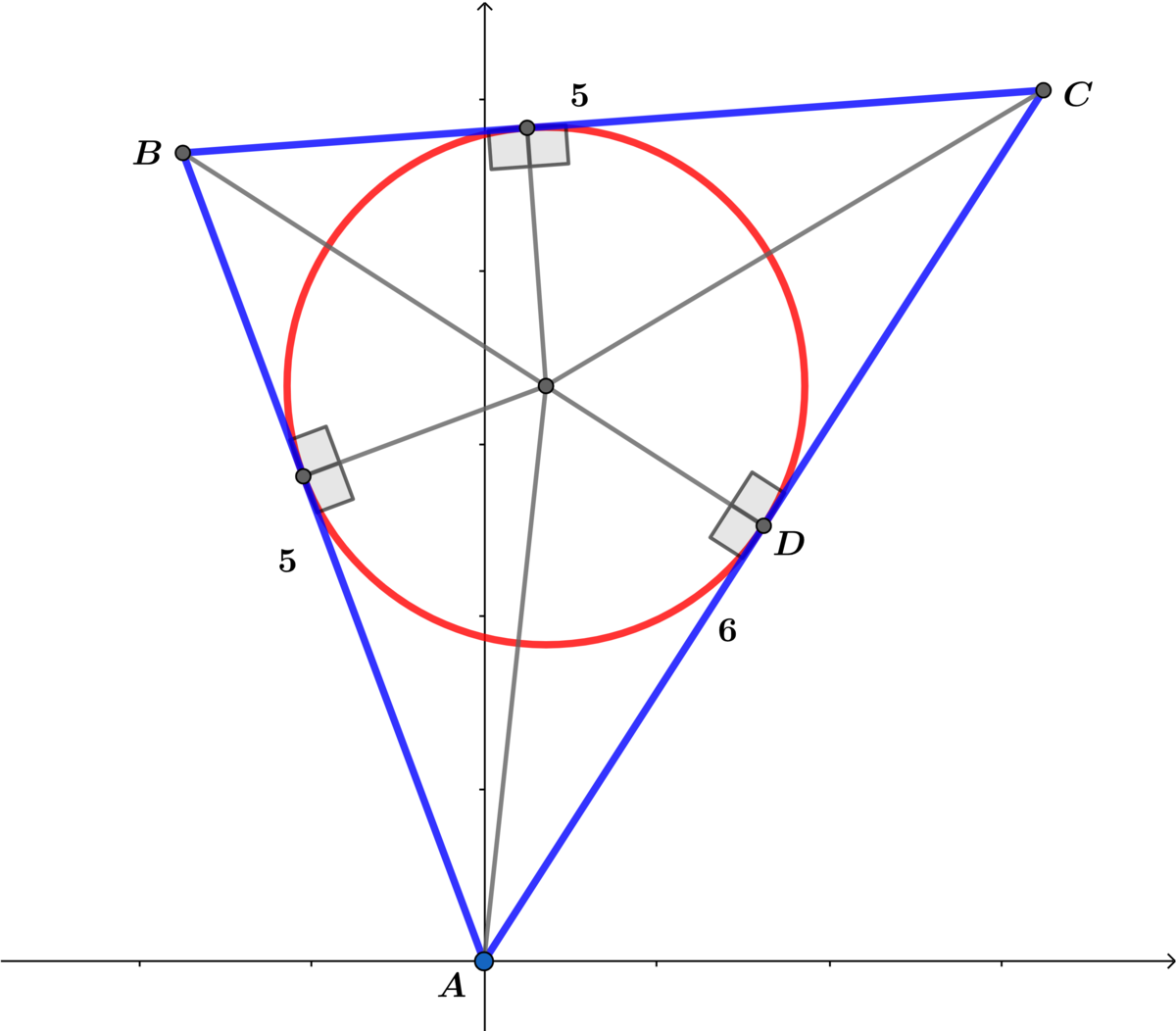
D is a midpoint of A C ⟹ D : ( 3 cos ( θ ) , 3 sin ( θ ) ) and from above
B : ( 3 cos ( θ ) − 4 sin ( θ ) , 4 cos ( θ ) + 3 sin ( θ ) ) ⟹ B D = 4
⟹
A △ A B C = 2 1 ( 6 ) ( 4 ) = 1 2 = 2 1 r ( 1 6 ) = 8 r ⟹ r = 2 3 ⟹ A c = 4 9 π = β α π
Since the result is a unique number, it is independent of θ , so, we can use any convenient value, like θ = 0 for instance. Then, we have the following three lines l 1 : 3 y − 4 x = 0 l 2 : 4 x + 3 y = 2 4 l 3 : y = 0 The rest is simple calculations: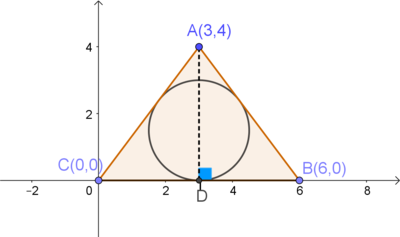 The intersection points of the lines are easily calculated
l
1
∩
l
2
≡
A
(
3
,
4
)
l
2
∩
l
3
≡
B
(
6
,
0
)
l
3
∩
l
1
≡
C
(
0
,
0
)
The perimeter of
△
A
B
C
defined by these points is
P
=
A
B
+
B
C
+
C
A
=
(
6
−
3
)
2
+
(
0
−
4
)
2
+
(
0
−
6
)
2
+
(
0
−
0
)
2
+
(
3
−
0
)
2
+
(
4
−
0
)
2
=
1
6
The area of the triangle is
[
A
B
C
]
=
2
1
B
C
⋅
d
(
A
,
B
C
)
=
2
1
×
6
×
4
=
1
2
For the radius of the incircle of
△
A
B
C
we have
r
=
2
1
P
[
A
B
C
]
=
8
1
2
=
2
3
Finally, the area of the incircle is
A
c
=
π
r
2
=
4
9
π
For the answer,
a
=
9
,
b
=
4
, thus,
A
+
B
=
1
3
.
The intersection points of the lines are easily calculated
l
1
∩
l
2
≡
A
(
3
,
4
)
l
2
∩
l
3
≡
B
(
6
,
0
)
l
3
∩
l
1
≡
C
(
0
,
0
)
The perimeter of
△
A
B
C
defined by these points is
P
=
A
B
+
B
C
+
C
A
=
(
6
−
3
)
2
+
(
0
−
4
)
2
+
(
0
−
6
)
2
+
(
0
−
0
)
2
+
(
3
−
0
)
2
+
(
4
−
0
)
2
=
1
6
The area of the triangle is
[
A
B
C
]
=
2
1
B
C
⋅
d
(
A
,
B
C
)
=
2
1
×
6
×
4
=
1
2
For the radius of the incircle of
△
A
B
C
we have
r
=
2
1
P
[
A
B
C
]
=
8
1
2
=
2
3
Finally, the area of the incircle is
A
c
=
π
r
2
=
4
9
π
For the answer,
a
=
9
,
b
=
4
, thus,
A
+
B
=
1
3
.