Circle inside a hexagon
A circle is inscribed in a hexagon, as shown in the diagram.
Is it possible that the side lengths of the hexagon are in some order?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
This problem is extremely similar in concept to the first problem from the Basic set for this week . In that problem, we wanted to know if it was possible for
to all be odd. With this problem, we want
to all be odd. The extra condition that is an odd number causes this case to fail.
Suppose yes. Then we will use the figure below.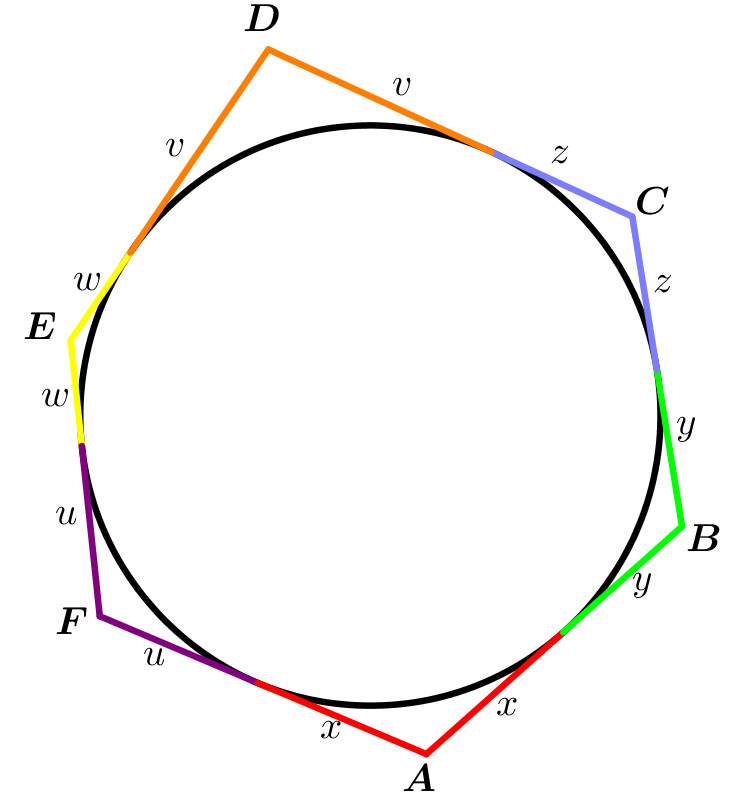
x + y + z + v + w + u = 2 ( x + y ) + ( y + z ) + ( z + v ) + ( v + w ) + ( w + u ) + ( u + x ) = 2 7 + 9 + 1 1 + 1 3 + 1 5 + 1 7 = 3 6
From that A B + C D + E F = x + y + z + v + w + z = 3 6 which is impossible, since the sum of three odd integers is always an odd number. (Note: The 7 , 9 , 1 1 , 1 3 , 1 5 , 1 7 are all odd integers.)
Therefore it is impossible.