Circle Mania!

By Descartes' theorem :

$\large -\cfrac{1}{r_1 + r_2} = \cfrac{1}{r_1} + \cfrac{1}{r_2} + \cfrac{1}{r_3} - 2\sqrt{\cfrac{1}{r_1r_2} + \cfrac{1}{r_1r_3} + \cfrac{1}{r_2r_3}}$

which rearranges to:

$r_3 = \cfrac{r_1r_2(r_1 + r_2)}{r_1^2 + r_1r_2 + r_2^2}$

Therefore, when $r_1 = 2$ and $r_2 = 1$ , $r_3 = \cfrac{2 \cdot 1 \cdot (2 + 1)}{2^2 + 2 \cdot 1 + 1^2} = \cfrac{6}{7} \approx \boxed{0.8571428571428571}$ .

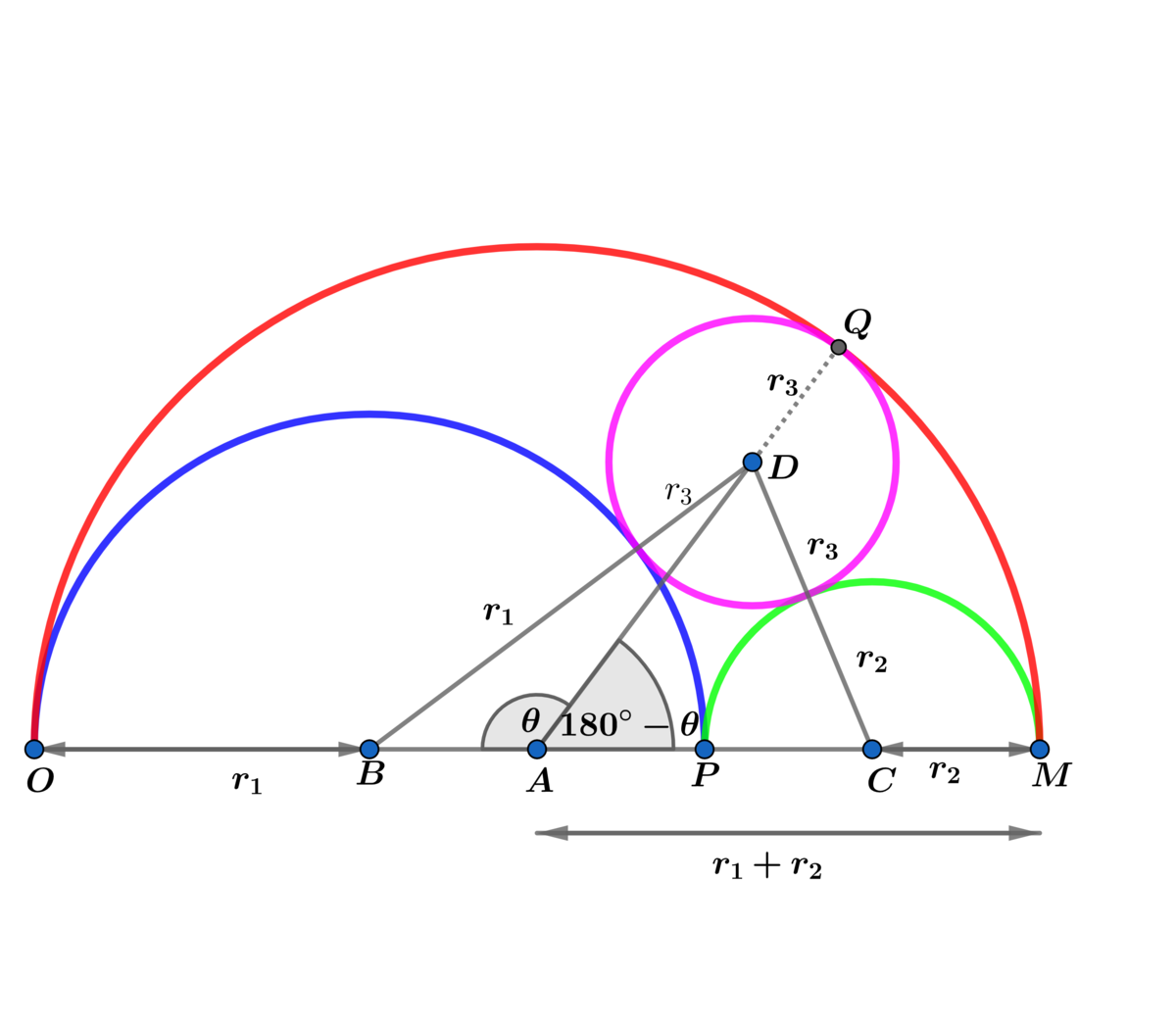
I am doing the problem in general, then replacing the given values $r_{1} = 2$ and $r_{2} = 1$ into the final result to obtain $r_{3}$ .

Let $r_{1} > r_{2}$ .

$\overline{OM} = 2(r_{1} + r_{2}) \implies \overline{AM} = r_{1} + r_{2} \implies \overline{AP} = r_{1} - r_{2} \implies \overline{AB} = r_{2}$ and

$\overline{AC} = r_{1}$ and $AD = r_{1} + r_{2} - r_{3}$

Using the law of cosines on $\triangle{BDA} \implies$

$(1): \:\ (r_{1} + r_{3})^2 = r_{2}^2 + (r_{1} + r_{2} - r_{3})^2 - 2r_{2}(r_{1} + r_{2} - r_{3})\cos(\theta)$

Using the law of cosines on $\triangle{ADC} \implies$

$(2): \:\ (r_{2} + r_{3})^2 = r_{1}^2 + (r_{1} + r_{2} - r_{3})^2 + 2r_{1}(r_{1} + r_{2} - r_{3})\cos(\theta)$

Multiplying $(1)$ by $r_{1}$ and $(2)$ by $r_{2}$ and adding we obtain:

$r_{1}^3 + 2r_{1}^2r_{3} + r_{1}r_{3}^2 + r_{2}^3 + 2r_{2}^2r_{3} + r_{2}r_{3}^2 =$

$4r_{1}^2r_{2} + 4r_{2}^2r_{1} - 4r_{1}r_{2}r_{3} + r_{1}^3 - 2r_{1}^2r_{3} -2r_{2}^2r_{3} + r_{2}^3 + r_{2}r_{3}^2 + r_{1}r_{3}^2$

$\implies r_{1}^2r_{3} + r_{2}^2r_{3} = r_{1}r_{2}^2 + r_{2}r_{1}^2 - r_{1}r_{2}r_{3} \implies$

$(r_{1}^2 + r_{1}r_{2} + r_{2}^2)r_{3} = r_{1}r_{2}(r_{1} + r_{2}) \implies \boxed{r_{3} = \dfrac{r_{1}r_{2}(r_{1} + r_{2})}{r_{2}^2 + r_{1}r_{2} + r_{2}^2}}$

Using $r_{1} = 2$ and $r_{2} = 1 \implies \boxed{r_{3} = \dfrac{6}{7} \approx 0.8571428571428571}$ .

We note that $AD=r_1+r_2 - r_3$ . $BD=r_1+r_3$ , and $CD=r_2+r_3$ . Let $A$ be the origin of the $xy$ -plane $(0,0)$ . Then the point $D(x,y)$ satisfies the following system of equations:

$\begin{cases} \begin{array} {lll} AD: & x^2 + y^2 = (r_1+r_2-r_3)^2 & \implies x^2 + y^2 = r_1^2+r_2^2+r_3^2 + 2(r_1r_2 -r_2r_3 - r_3r_1) & ...(1) \\ BD: & (x+r_2)^2 + y^2 = (r_1+r_3)^2 & \implies x^2 + 2r_2x + r_2^2 + y^2 = r_1^2 + 2r_3r_1 + r_3^2 & ...(2) \\ CD: & (x-r_1)^2 + y^2 = (r_2+r_3)^2 & \implies x^2 - 2r_1x + r_1^2 + y^2 = r_2^2 + 2r_2r_3 + r_3^2 & ...(3) \end{array} \end{cases}$

$\begin{aligned} (2)-(1): \quad 2r_2 x + r_2^2 & = - r_2^2 - 2r_1r_2 + 2r_2r_3 + 4r_3r_1 \\ \implies x & = -r_1 - r_2 + r_3 + \frac {2r_3r_1}{r_2} & ...(4) \\ (1)-(3): \quad 2r_1x - r_1^2 & = r_1^2 + 2r_1r_2 - 4r_2r_3 - 2r_3r_1 \\ \implies x & = r_1 + r_2 - r_3 - \frac {2r_2r_3}{r_1} & ...(5) \end{aligned}$

$\begin{aligned} (5)-(4): \hspace{1in} 0 & = 2r_1 + 2r_2 - 2r_3 - 2r_3 \left(\frac {r_2}{r_1} + \frac {r_1}{r_2} \right) \\ r_3 \left(\frac {r_1^2+r_1r_2+r_2^2}{r_1r_2} \right) & = r_1 + r_2 \\ \implies r_3 & = \frac {r_1r_2(r_1+r_2)}{r_1^2+r_1r_2+r_2^2} \end{aligned}$

For $r_1 = 2$ and $r_2 = 1$ , we have $r_3 = \dfrac {2\cdot 1(2+1)}{2^2+2\cdot 1 + 1^2} = \dfrac 67 \approx \boxed{0.857}$ .