Circle Mania

Geometry Level pending

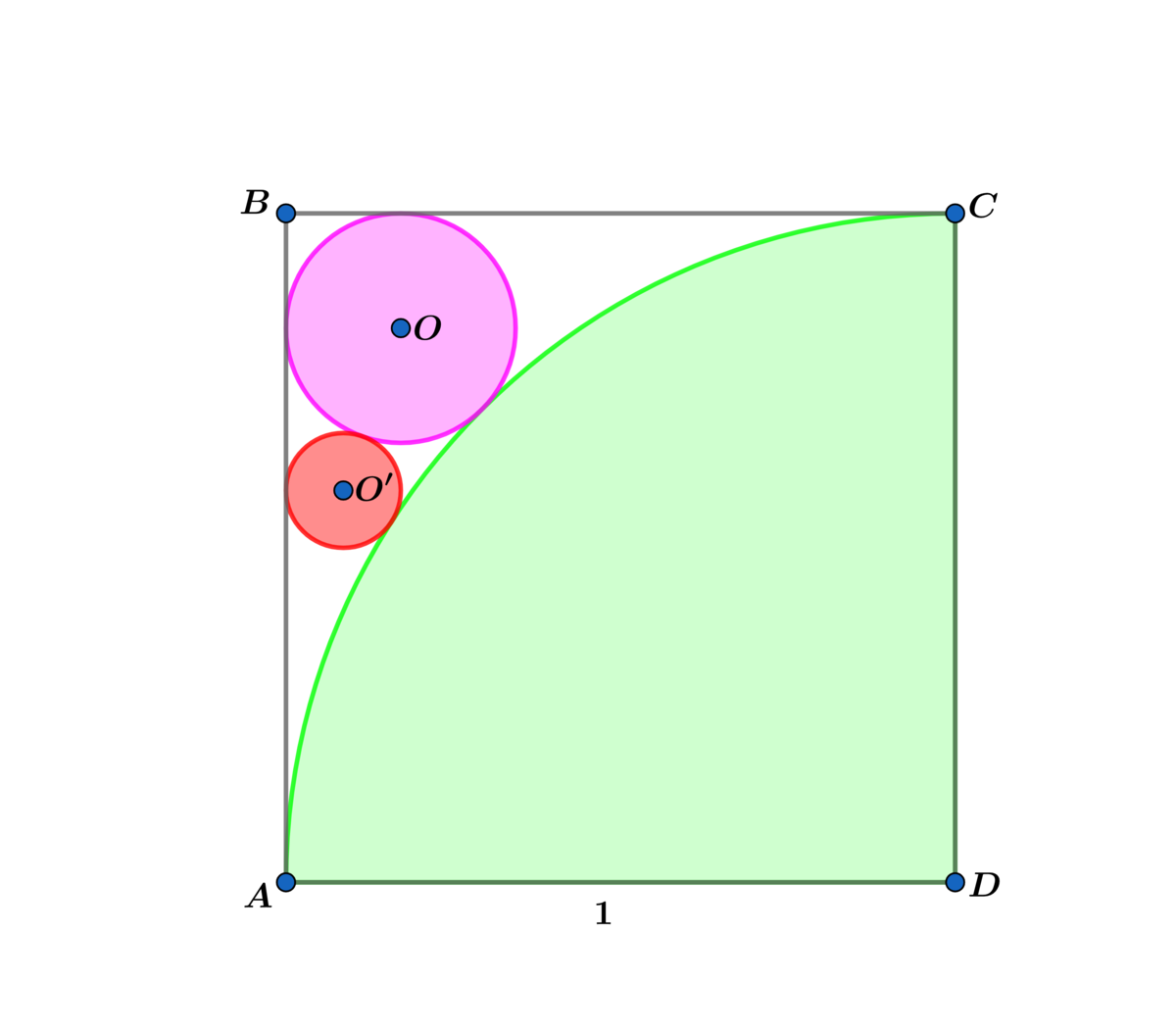
In the diagram above square A B C D ABCD has side length 1 1 . If the pink and red circle are tangent to each other and tangent to the green circle and B C ‾ \overline{BC} is tangent to the pink circle and A B ‾ \overline{AB} is tangent to the pink and red circle.

If the radius of the red circle r = α − β β β r = \dfrac{\alpha - \beta\sqrt{\beta}}{\beta} , where α \alpha and β \beta are coprime positive integers, find α + β \alpha + \beta .


The answer is 5.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Hongqi Wang
Jan 25, 2021

The length of diagonal: ( 2 + 1 ) r p + r g = 2 a ⟹ ( 2 + 1 ) r p + 1 = 2 r p = 2 − 1 2 + 1 = 1 ( 2 + 1 ) 2 \begin{aligned} \\ &(\sqrt 2 + 1)r_{p} + r_{g} = \sqrt 2 a \\ \implies &(\sqrt 2 + 1)r_p + 1 = \sqrt 2 \\ r_p &= \dfrac {\sqrt 2 - 1}{\sqrt 2 + 1} = \dfrac 1{(\sqrt 2 + 1)^2} \end{aligned}

line A B AB can be taken as a circle with radius ∞ \infty . Then with Descartes' theorem: k r = k g + k p + k A B − 2 k g k p + k p k A B + k A B k g = 1 + ( 2 + 1 ) 2 + 0 − 2 1 ⋅ ( 2 + 1 ) 2 + ( 2 + 1 ) 2 ⋅ 0 + 0 ⋅ 1 = 6 + 4 2 ∴ r r = 1 k r = 3 − 2 2 2 \\ k_r = k_g + k_p + k_{AB} -2\sqrt {k_g k_p + k_p k_{AB} + k_{AB} k_g} \\ = 1 + (\sqrt 2 + 1)^2 + 0 - 2 \sqrt {1 \cdot (\sqrt 2 + 1)^2 + (\sqrt 2 + 1)^2 \cdot 0 + 0 \cdot 1} \\ = 6 + 4 \sqrt 2 \\ \therefore r_r = \dfrac 1{k_r} = \dfrac {3 - 2 \sqrt 2}{2}

2 Helpful 1 Interesting 1 Brilliant 0 Confused
Rocco Dalto
Jan 23, 2021

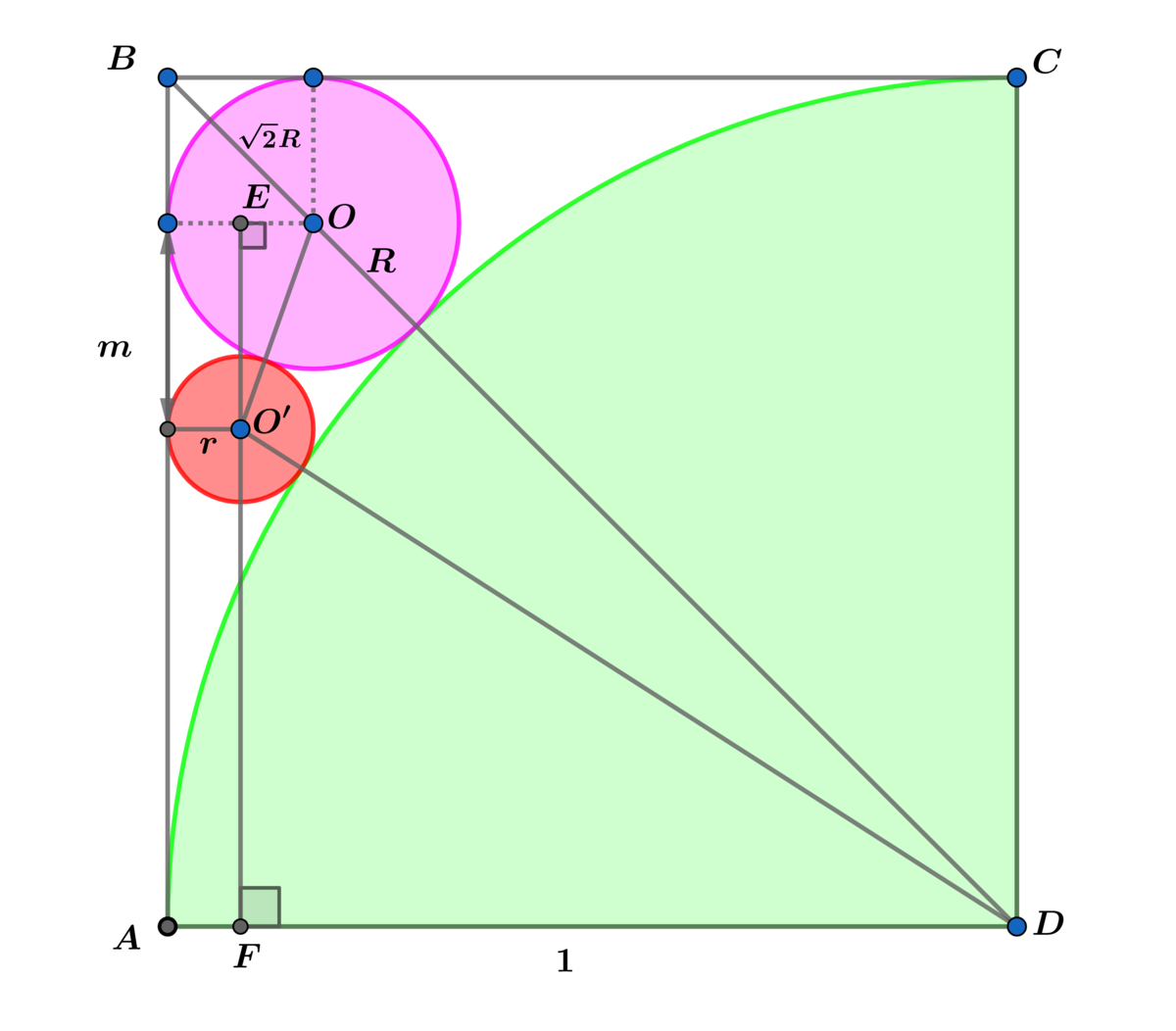
B D ‾ = 2 = 1 + R + 2 R = 1 + ( 2 + 1 ) R ⟹ R = 2 − 1 2 + 1 = 3 − 2 2 \overline{BD} = \sqrt{2} = 1 + R + \sqrt{2}R = 1 + (\sqrt{2} + 1)R \implies R = \dfrac{\sqrt{2} - 1}{\sqrt{2} + 1} = 3 - 2\sqrt{2}

Using △ O ′ E O ⟹ m 2 = ( R + r ) 2 − ( R − r ) 2 = 4 R r ⟹ m = 2 R r \triangle{O'EO} \implies m^2 = (R + r)^2 - (R - r)^2 = 4Rr \implies m = 2\sqrt{Rr}

and

Using △ F O ′ D ⟹ ( 1 + r ) 2 = ( 1 − r ) 2 + ( 1 − R − m ) 2 ⟹ \triangle{FO'D} \implies (1 + r)^2 = (1- r)^2 + (1 - R - m)^2 \implies

4 r = ( 1 − R ) 2 − 2 m ( 1 − r ) + m 2 = ( 1 − R ) 2 − 4 ( 1 − R ) R r + 4 R r ⟹ 4r = (1 - R)^2 - 2m(1 - r) + m^2 = (1 - R)^2 - 4(1 - R)\sqrt{Rr} + 4Rr \implies

4 ( 1 − R ) r = ( 1 − R ) 2 − 4 R r ( 1 − R ) ⟹ 4 r = 1 − R − 4 R r ⟹ 4(1 - R)r = (1 - R)^2 - 4\sqrt{Rr}(1 - R) \implies 4r = 1 - R - 4\sqrt{Rr} \implies

4 r + 4 R r + R = 1 ⟹ ( R + 2 r ) 2 = 1 ⟹ R + 2 r = 1 ⟹ 4r + 4\sqrt{Rr} + R = 1 \implies (\sqrt{R} + 2\sqrt{r})^2 = 1 \implies \sqrt{R} + 2\sqrt{r} = 1 \implies

r = 1 − R 2 = 1 − 3 − 2 2 2 = 1 − ( 2 − 1 ) 2 2 = 2 − 2 2 = 2 ( 2 − 1 ) 2 \sqrt{r} = \dfrac{1 - \sqrt{R}}{2} = \dfrac{1 - \sqrt{3 - 2\sqrt{2}}}{2} = \dfrac{1 - \sqrt{(\sqrt{2} - 1})^2}{2} = \dfrac{2 - \sqrt{2}}{2} = \dfrac{\sqrt{2}(\sqrt{2} - 1)}{2}

⟹ r = 2 ( 3 − 2 2 ) 4 = 3 − 2 2 2 = α − β β β ⟹ α + β = 5 \implies r = \dfrac{2(3 - 2\sqrt{2})}{4} = \dfrac{3 - 2\sqrt{2}}{2} = \dfrac{\alpha - \beta\sqrt{\beta}}{\beta} \implies \alpha + \beta = \boxed{5} .

2 Helpful 2 Interesting 2 Brilliant 0 Confused

I solved it with the law of cosines for triangle DOO' but it's unbelievably messy. Still, got the same answer. Nice problem, enjoyed it!

Veselin Dimov - 4 months, 2 weeks ago

Thanks. Your right, the algebra is tedious.

Rocco Dalto - 4 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...