Circle Mania 2.
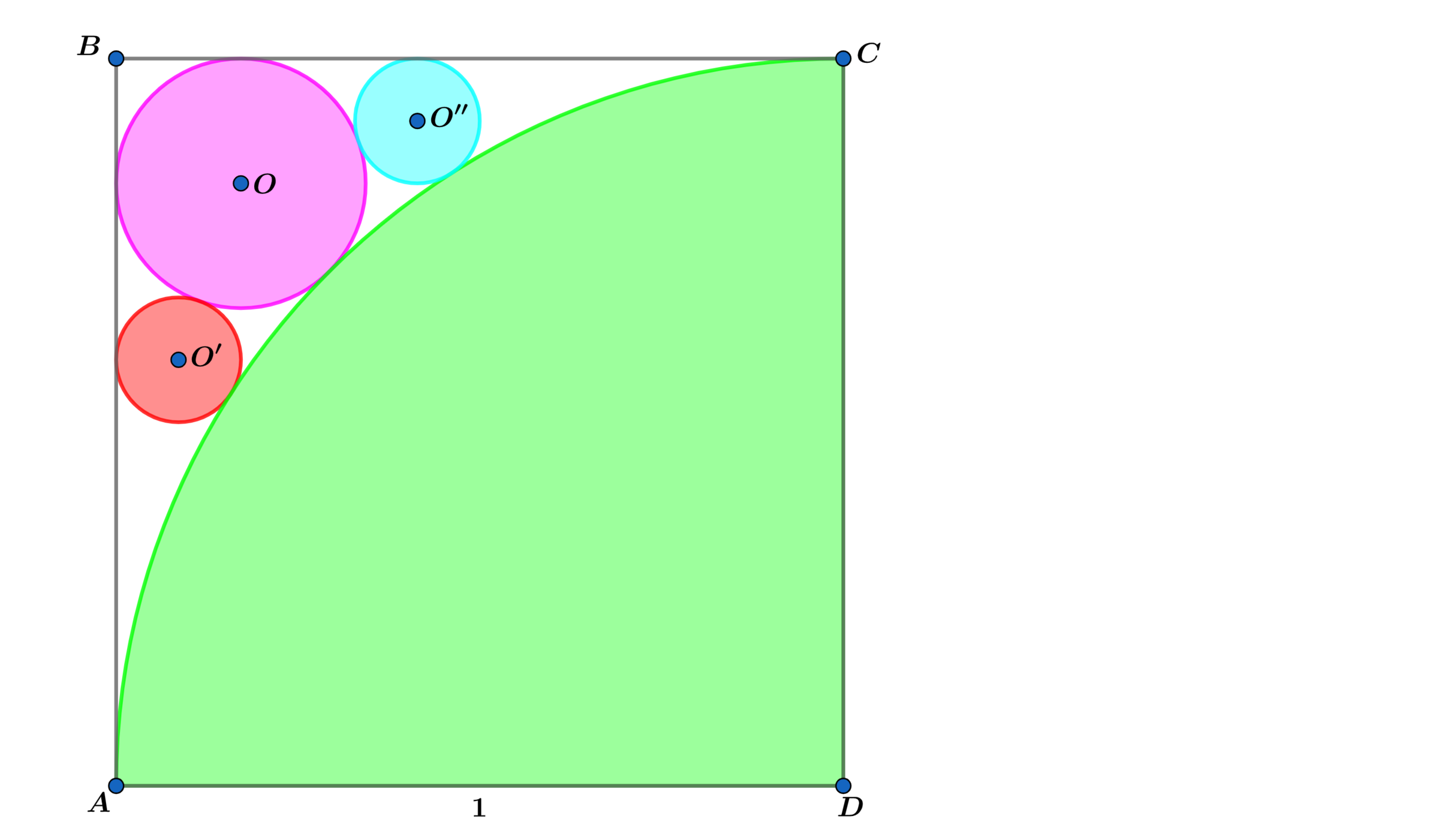
In the diagram above square A B C D has side length 1 and the pink, red and blue circle are tangent to each other and tangent to the green circle and B C is tangent to the pink circle and blue circle and A B is tangent to the pink and red circle.
Let S be the sum of the areas of the pink, red and blue circles.
If S = β α π ( λ − ω β ) , where α , β , λ and ω are coprime positive integers, find α + β + λ + ω .
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the radius of the pink circle be R and the radius of the red and blue circles be r . Add E and F as follows:
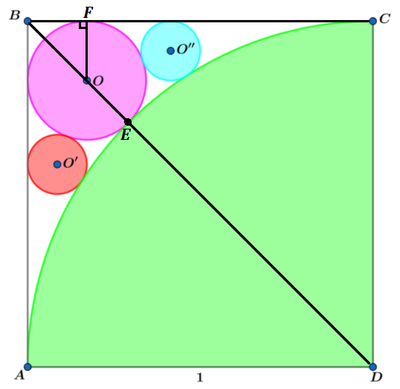
As a diagonal of a unit square, B D = 2 . As a hypotenuse of right △ B F O with O F = R , B O = 2 R . Therefore, B D = B O + O E + E D = 2 R + R + 1 = 2 , which solves to R = 3 − 2 2 .
By Descartes' Theorem (special case with a straight line), r 1 = 1 + R 1 + 2 1 ⋅ R 1 = 1 + 3 − 2 2 1 + 2 1 ⋅ 3 − 2 2 1 = 3 − 2 2 2 , so that r = 2 1 ( 3 − 2 2 ) .
Therefore, S = π R 2 + 2 π r 2 = π ( ( 3 − 2 2 ) 2 + 2 ( 2 1 ( 3 − 2 2 ) ) 2 ) = 2 3 ( 1 7 − 1 2 2 ) , so α = 3 , β = 2 , λ = 1 7 , ω = 1 2 , and α + β + λ + ω = 3 4 .
r p i n k = 3 − 2 2 r r e d = r b l u e = 2 3 − 2 2 = 2 r p i n k S = π ( r p i n k 2 + r r e d 2 + r b l u e 2 ) = 2 3 π r p i n k 2 = 2 3 π ( 3 − 2 2 ) 2 = 2 3 π ( 1 7 − 1 2 2 )
Note: We just need to find R then r since r = r ′ using the symmetry about B D .
B D = 2 = 1 + R + 2 R = 1 + ( 2 + 1 ) R ⟹ R = 2 + 1 2 − 1 = 3 − 2 2
Using △ O ′ E O ⟹ m 2 = ( R + r ) 2 − ( R − r ) 2 = 4 R r ⟹ m = 2 R r
and
Using △ F O ′ D ⟹ ( 1 + r ) 2 = ( 1 − r ) 2 + ( 1 − R − m ) 2 ⟹
4 r = ( 1 − R ) 2 − 2 m ( 1 − r ) + m 2 = ( 1 − R ) 2 − 4 ( 1 − R ) R r + 4 R r ⟹
4 ( 1 − R ) r = ( 1 − R ) 2 − 4 R r ( 1 − R ) ⟹ 4 r = 1 − R − 4 R r ⟹
4 r + 4 R r + R = 1 ⟹ ( R + 2 r ) 2 = 1 ⟹ R + 2 r = 1 ⟹
r = 2 1 − R = 2 1 − 3 − 2 2 = 2 1 − ( 2 − 1 ) 2 = 2 2 − 2 = 2 2 ( 2 − 1 )
⟹ r = 4 2 ( 3 − 2 2 ) = 2 3 − 2 2 = 2 R ⟹ S = π R 2 + 2 π ( 2 R ) 2 =
2 3 π ( 3 − 2 2 ) 2 = 2 3 π ( 1 7 − 1 2 2 ) = β α π ( λ − ω β ) ⟹ α + β + λ + ω = 3 4 .