Circle Meets Parabola at the Triangle Bar
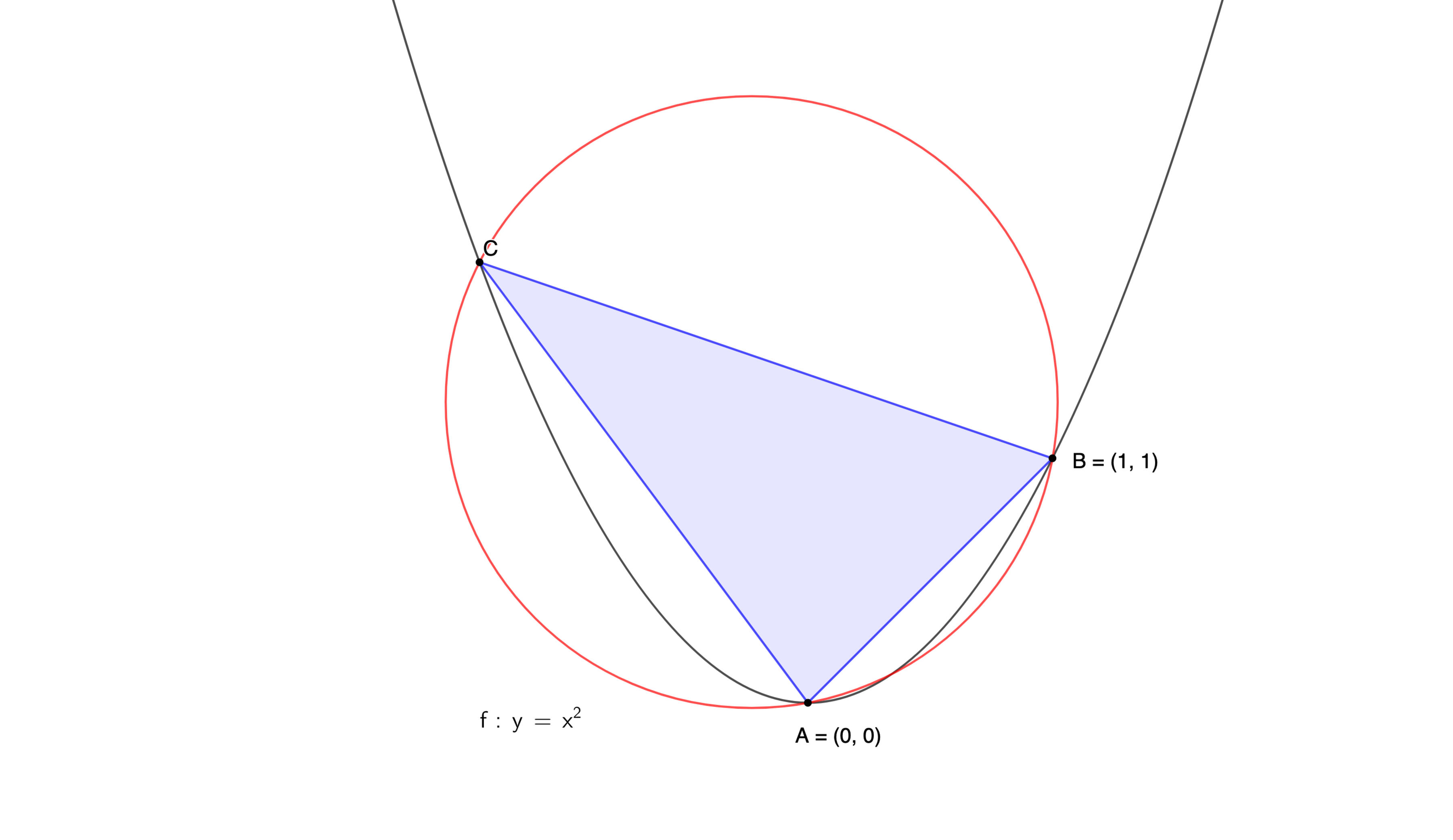
Three points, A , B , C lie on the parabola y = x 2 . A is ( 0 , 0 ) , B is ( 1 , 1 ) and C can lie anywhere else, i.e. it is not restricted to being to the left of A . Find the triangles's smallest circumcircle (red).
If the radius is expressed as c a b , where a , b , c are positive integers with a , c coprime and b square-free, submit a + b + c .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Exactly the same approach.
Let C have coordinates ( t , t 2 ) .
The triangle's circumcentre lies at the intersection of the perpendicular bisectors of its sides.
The perpendicular bisector of A B is the line y = 1 − x
The perpendicular bisector of A C is the line x − 2 1 t y − 2 1 t 2 = − t 1
The intersection of these is the point P ( − 2 1 t ( t + 1 ) , 2 1 ( t 2 + t + 2 ) )
The circumradius is the distance from any of the triangle vertices to P ; it's easiest to look at A P . After going through the paperwork, we find R 2 = 2 1 ( t 2 + 1 ) ( t 2 + 2 t + 2 )
(as is often the case, it's easier to work with R 2 than R .)
This achieves a minimum value of 3 2 2 5 when t = − 2 1 . Taking the square root, we find R = 8 5 2
for an answer of 1 5 .
Let the coordinates of C be ( k , k 2 ) . Then by the distance formula:
a = B C = ( k − 1 ) 2 + ( k 2 − 1 ) 2 = k 4 − k 2 − 2 k + 2
b = A C = ( k − 0 ) 2 + ( k 2 − 0 ) 2 = k 4 + k 2
c = A B = ( 1 − 0 ) 2 + ( 1 − 0 ) 2 = 2 .
By Heron's formula , the area of △ A B C is:
T = 4 1 4 a 2 b 2 − ( a 2 + b 2 − c 2 ) 2 = 4 1 4 ( k 4 − k 2 − 2 k + 2 ) ( k 4 + k 2 ) − ( ( k 4 − k 2 − 2 k + 2 ) + ( k 4 + k 2 ) − 2 ) 2 = 2 1 k ( k − 1 ) .
The square of the circumradius is:
R 2 = 1 6 T 2 a 2 b 2 c 2 = 1 6 ⋅ 4 1 k 2 ( k − 1 ) 2 ( k 4 − k 2 − 2 k + 2 ) ( k 4 + k 2 ) ( 2 ) = 2 1 k 4 + k 3 + 2 3 k 2 + k + 1
By implicit differentiation, 2 R ⋅ d k d R = 2 k 3 + 3 k 2 + 3 k + 1 . The minimum occurs when d k d R = 0 (and when d k 2 d 2 R > 0 ), so 0 = 2 k 3 + 3 k 2 + 3 k + 1 , which has one real solution of k = − 2 1 .
When k = − 2 1 , R 2 = 2 1 k 4 + k 3 + 2 3 k 2 + k + 1 = 2 1 ( − 2 1 ) 4 + ( − 2 1 ) 3 + 2 3 ( − 2 1 ) 2 + ( − 2 1 ) + 1 = 3 2 2 5 , so R = 3 2 2 5 = 8 5 2 .
Therefore, a = 5 , b = 2 , c = 8 , and a + b + c = 1 5 .
We note that diameter of a circumcircle is given by 2 r = sin C c . In this case c = A B = 2 . We need to find the largest sin C to find the smallest r .
Let C ( x , x 2 ) and ∠ C = θ . Then
θ tan θ ⟹ sin θ ⟹ max ( sin θ ) ⟹ r min = tan − 1 x − 1 x 2 − 1 − tan − 1 x x 2 = tan − 1 ( x + 1 ) − tan − 1 x = 1 + x ( x + 1 ) x + 1 − x = x 2 + x + 1 1 = ( x 2 + x + 1 ) 2 + 1 1 = ( ( x + 2 1 ) 2 + 4 3 ) 2 + 1 1 = ( 0 + 4 3 ) 2 + 1 1 = 5 4 = 2 max ( sin θ ) 2 = 8 5 2 when x = − 2 1
Therefore a + b + c = 5 + 2 + 8 = 1 5 .