Circle on a Strip

First, place everything on the coordinate plane, with point $P$ as the origin and the two edges of the paper as $y=-\dfrac{1}{4}$ and $y=\dfrac{3}{4}$ . Consider the edges separately:

If a circle can be drawn with center $O$ passing through $P$ and not intersecting $y=-\dfrac{1}{4}$ , then we know that $\overline{OP}\ge \overline{OH}$ where $H$ is the perpendicular from $O$ to the line $y=-\dfrac{1}{4}$ .

But this means that $O$ lies above the parabola with focus $P$ and directrix $y=-\dfrac{1}{4}$ , recalling that the definition of a parabola is $OP=OH$ .

Similarly, $O$ lies below the parabola with focus $P$ and directrix $y=\dfrac{3}{4}$ .

These two parabolas have equations $y=2x^2-\dfrac{1}{8}$ $y=-\dfrac{2}{3}x^2+\dfrac{3}{8}$

It remains to find the area between these two curves, which can be found using calculus.

First, turn finding the area between two curves to only one curve by subtracting: $\left(-\dfrac{2}{3}x^2+\dfrac{3}{8}\right)-\left(2x^2-\dfrac{1}{8}\right)=\dfrac{1}{2}-\dfrac{8}{3}x^2$

To find the area of the region bounded by this curve and the x-axis, we first find the roots of the quadratic: $\dfrac{1}{2}-\dfrac{8}{3}x^2\iff x^2=\dfrac{3}{16}\iff x=\dfrac{\sqrt{3}}{4}$

And thus our answer is $\int_{-\frac{\sqrt{3}}{4}}^{\frac{\sqrt{3}}{4}}\dfrac{1}{2}-\dfrac{8}{3}x^2\text{ d}x=\left.\dfrac{1}{2}x-\dfrac{8}{9}x^3\right|_{-\frac{\sqrt{3}}{4}}^{\frac{\sqrt{3}}{4}}=\dfrac{\sqrt{3}}{6}$

So out answer is $1+3+6=\boxed{10}$

Consider a polar coordinate function in which our radius $r$ is the distance from the point $P$ to the locus of points $L$ for a given $\theta$ . To begin, allow our point $P$ to be the center point, and WLOG the point $P$ is located $\frac{1}{4}$ units away from the top of the strip.

Imagine you are starting at your point $P$ slowly extending the radius outward in the direction of our $\theta$ , and as our radius extends so does the circle that it creates. We extend our radius and allow our circle to grow until it hits either the top or the bottom of the paper.

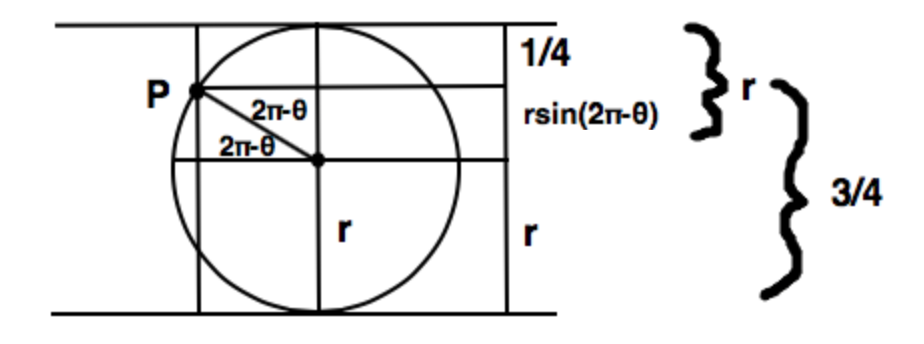
Our formula for $r$ actually must have two equations, one that accounts for when the circle hits the top of the paper and one when it hits the bottom. The image above is of one of the two points where the circle is tangent to both the top of the paper and the bottom of the paper. Since it touches both sides we can use is to determine our two equations for $r$ .

Equation 1 corresponds with the circle hitting the top:

$\frac{1}{4}+r\sin{(2π-\theta)}=r$

$\frac{1}{4}-r\sin{\theta}=r$

$r(1+\sin{\theta})=\frac{1}{4}$

$r = \frac{1}{4(1+\sin{\theta})}$

Equation 2 corresponds with the circle hitting the bottom:

$r+r\sin{(2π-\theta)}=\frac{3}{4}$

$r-r\sin{\theta}=\frac{3}{4}$

$r(1-\sin{\theta})=\frac{3}{4}$

$r = \frac{3}{4(1-\sin{\theta})}$

Now we need to find the points at which the circle stops hitting the top and starts hitting the bottom, and vice-versa. Setting the two equations equal to each other yields the answers.

$\frac{1}{4(1+\sin{\theta})}=\frac{3}{4(1-\sin{\theta})}$

$1-\sin{\theta}=3+3\sin{\theta}$

$4\sin{\theta}=-2$

$\sin{\theta}=\frac{-1}{2} \Longrightarrow \theta=\{\frac{7π}{6},\frac{11π}{6}\}$

We can see now that our image above is at the point where $\theta=\frac{11π}{6}$ . It is clear that as $\theta$ increases from this point that the circle will hit the top first, so we know now that we must evaluate our first equation on the interval $(\frac{-π}{6},\frac{7π}{6})$ and our second equation on the interval $(\frac{7π}{6},\frac{11π}{6})$ .

So how can we find the area of the entire locus of points? All we have left to do is integrate each function over they're specific intervals and sum the two values together. To integrate a polar function we use the following formula:

$\frac{1}{2} \displaystyle\int_{a}^{b} r^2 d\theta$

$\frac{1}{32}\Bigg[\displaystyle\int_{\frac{-π}{6}}^{\frac{7π}{6}} \frac{1}{(1+\sin{\theta})^2} \theta+\displaystyle\int_{\frac{7π}{6}}^{\frac{11π}{6}} \frac{9}{(1-\sin{\theta})^2} d\theta\Bigg]$

$\frac{1}{32}\big[2\sqrt{3}+\frac{10}{\sqrt{3}}\big] = \frac{1\sqrt{3}}{6}$

Finally, our answer simplifies to $1+3+6=\boxed{10}$