Circle Problem
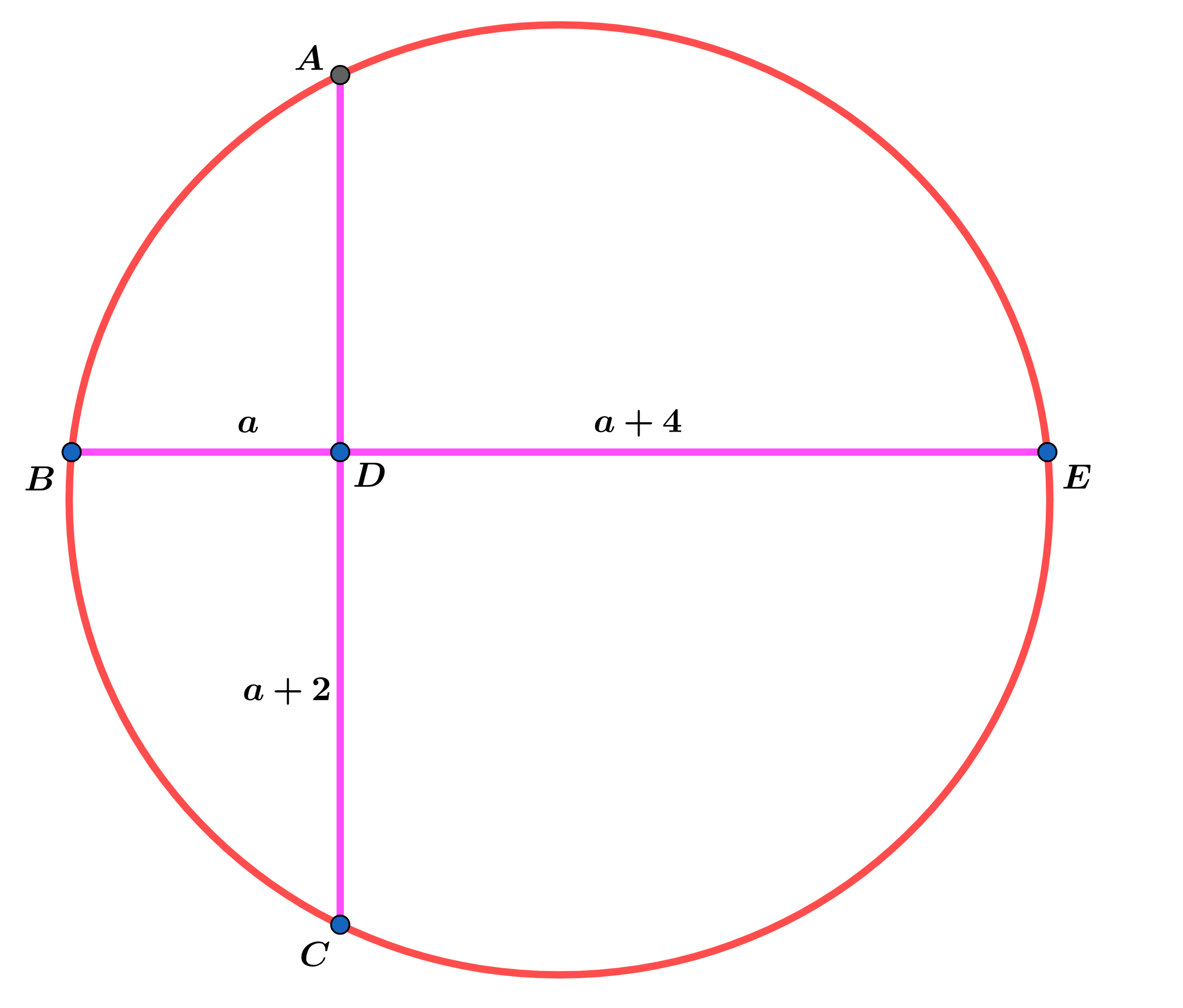
In the circle above chords A C and B E intersect at D , where B D = a , D E = a + 4 and D C = a + 2 .
If the radius of the circle r = 2 5 and a can be expressed as a = α β + α α α λ − α , where α , β and λ are coprime positive integers, find α + β + λ .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
a = 6
Log in to reply
Thanks. You should also inform @Rocco Dalto , who set the problem.
Log in to reply
I didn't realize that ( 2 + 6 ) 2 = 4 + 4 6 + 6 = 1 0 + 4 6 ⟹ 2 + 6 = 1 0 + 4 6 .
Although, I stated in the problem that a can be expressed as a = α β + α α α λ − α so that the problem is still correct.
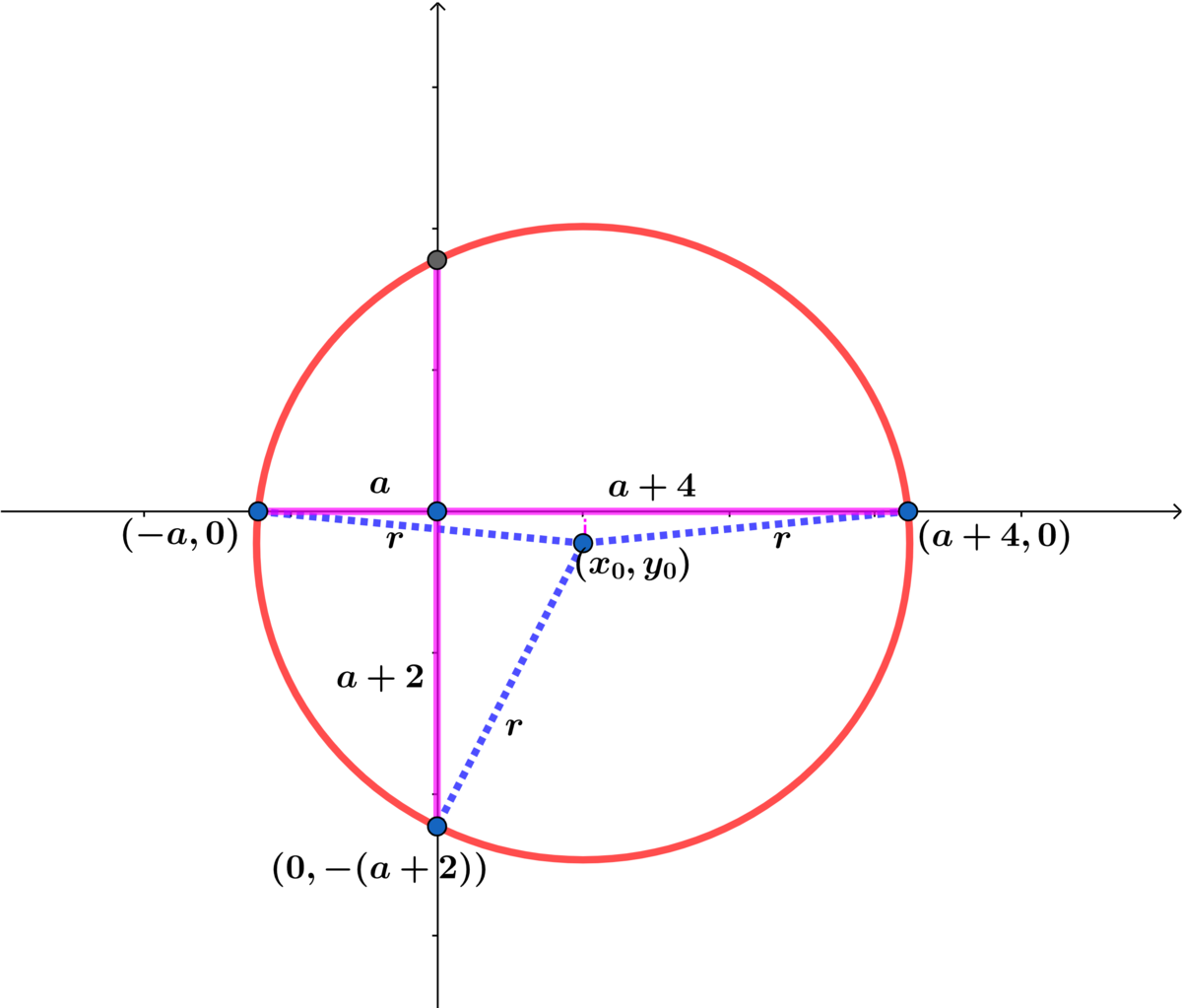
Let ( x 0 , y 0 ) be the center of the circle.
x 0 − ( a + 4 ) ) 3 + y 0 2 = r 2
( x 0 + a ) 2 + y 0 2 = r 2
Subtracting the two equations we obtain:
4 ( a + 2 ) x 0 = 8 ( a + 2 ) ⟹ x 0 = 2 .
For y 0 :
Using x 0 = 2 we have:
( a + 2 ) 2 + y 0 2 = r 2
4 + ( y 0 + ( a + 2 ) ) 2 = r 2
Subtracting the two equations we obtain:
− 2 ( a + 2 ) y 0 = 4 ⟹ y 0 = a + 2 − 2
⟹
( a + 2 ) 2 + ( a + 2 ) 2 4 = 2 0 ⟹ ( a + 2 ) 4 − 2 0 ( a + 2 ) 2 − 4 = 0 ⟹
a = ± 1 0 ± 4 6 − 2
The only positive real root is a = 1 0 + 4 6 − 2 = 2 ∗ 5 + 2 2 2 ∗ 3 − 2 =
α ∗ β + α α α ∗ λ − α ⟹ α + β + λ = 1 0 .
Let the center of the circle be the origin O ( 0 , 0 ) and the line B E is b above O . Then in coordinates, E ( a + 2 , b ) and C ( − 2 , b − ( a + 2 ) ) . By Pythagorean theorem, we have:
{ O E 2 : O C 2 : ( a + 2 ) 2 + b 2 = r 2 ( − 2 ) 2 + ( b − ( a + 2 ) ) 2 = r 2
⟹ ( a + 2 ) 2 + b 2 ⟹ 2 b ( a + 2 ) b = 4 + ( b − ( a + 2 ) ) 2 = 4 + b 2 − 2 b ( a + 2 ) + ( a + 2 ) 2 = 4 = a + 2 2
Putting in O E 2 :
( a + 2 ) 2 + ( a + 2 ) 2 4 = r 2 ( a + 2 ) 4 − 2 0 ( a + 2 ) 2 + 4 ⟹ ( a + 2 ) 2 a = 0 = 2 2 0 + 2 0 2 − 1 6 = 1 0 + 4 6 = 1 0 + 4 6 − 2 = 2 + 6 − 2 = 6 In response to Peter Csorba’s comments
Therefore α + β + γ = 2 + 5 + 3 = 1 0 .