Circle Shadow
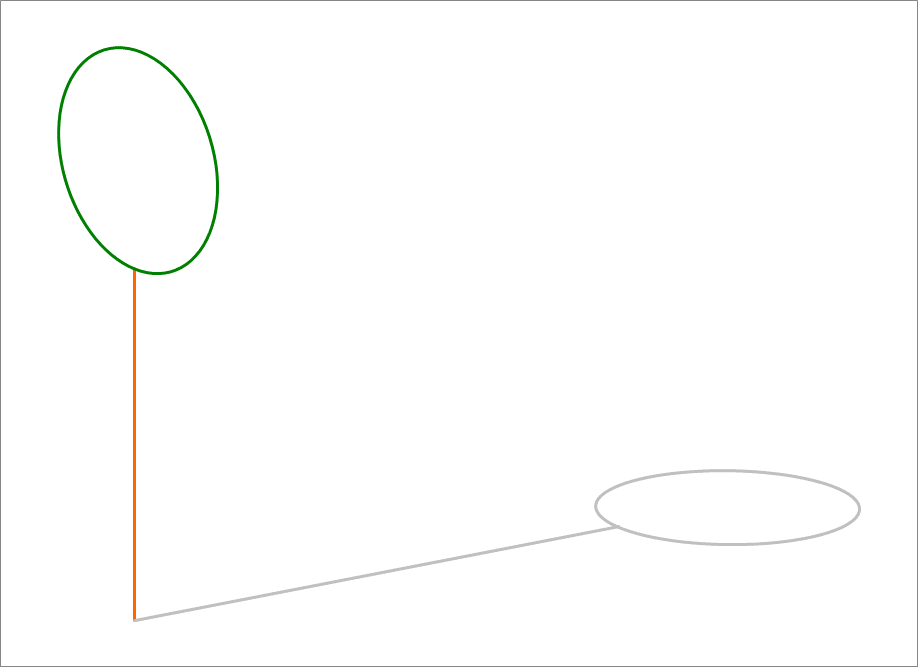
A circle of radius 10 units is centered at . The plane it lies in, has a normal vector . A uniform direction ray of light falls on the circle, generating a shadow on the floor (which is the XY plane). The direction of the shadow is given by . The shadow is an ellipse. Find the sum of the semi-major and semi-minor axes of this ellipse.
The answer is 24.267.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Points on the circle can be represented as
r C = r 0 + V u
where r 0 is the center of the circle and V = [ v 1 , v 2 ] , where v 1 , v 2 are two orthogonal vectors of length 10 that are orthogonal to the normal to the plane of the circle, and u = [ cos t , sin t ] T .
The equation of the projection plane is
n p T ( r − r p ) = 0
Now the projected point is generated from the original point on the circle as follows
r ′ = r C + t d
Hence,
n p T ( r c + t d − r p ) = 0
Therefore,
t ( n p T d ) + n p T ( r C − r p ) = 0
which implies,
t = − n p T d n p T ( r C − r p )
Therefore, the projected point onto the plane is given by,
r ′ = r C − n p T d n p T ( r C − r p ) d
r ′ = r C − n p T d d n p T ( r C − r p )
r ′ = r p + ( I − n p T d d n p T ) ( r C − r p )
which can written in compact form as:
r ′ = r p + P ( r C − r p )
with P = I − n p T d d n p T .
Next, we note that points on the projection plane can be represented by
r = r p + R p w
where R p is a 3 × 3 matrix comprising a reference frame attached to the projection plane and has its origin at r p . In particular,
R p = [ u 1 , u 2 , n p ]
where n p is the unit vector normal to the plane, and u 1 , u 2 are two orthogonal unit vectors that are also orthogonal to n p .
w is the coordinate of a given point with respect to this frame. Therefore,
r ′ = r p + P ( r C − r p ) = r p + R p w
Simplifying and substituting r C , we have
P ( r 0 + V u − r p ) = R p w
Solving for w , and noting that R p − 1 = R p T , we get,
w = R p T P ( r 0 − r p ) + R p T P V u
Define
h = R p T P ( r 0 − r p ) and G = R p T P V , then
w = h + G u
One can verify that the third row of R p T P is a row of zeros, making the third row of h and G a row of zeros as well. This is consistent with the fact that the third element of w should be zero, because the projected point lies in the projection plane. We will therefore consider only the first two rows of the above equation, thus obtaining,
w ′ = h ′ + G ′ u
where the primed variables are obtained from the original variables by taking only the first two rows.
Now, using the fact that u T u = 1 , we get
( w ′ − h ′ ) T G ′ − T G ′ − 1 ( w ′ − h ′ ) = 1
At this point we can find a rotation matrix R , and a diagonal matrix D such that
R T G ′ − T G ′ − 1 R = D
Therefore, by a change of variable, w ′ = R p + h ′ , we obtain
p T D p = 1
This is an equation of an ellipse, with semi-major and semi-minor axes given by the reciprocal of the square roots of the diagonal elements of D.
Performing the necessary calculations, we find that the semi-major axis M, and the semi-minor axis m, are given by
M = 1 5 . 8 6 0 2 9 6
m = 8 . 4 0 6 7 3 6 5
Therefore, the answer is M + m = 2 4 . 2 6 7